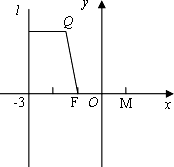
题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
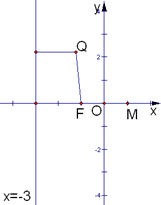
解:设点Q(x,y)(x>-3),由题意有x+3+ 整理得y2=-4xxÎ (-3,0] ∴动点Q的轨迹C为以F(-1,0)为焦点,坐标原点为顶点的抛物线在直线x=-3右侧的部分.(6分) |
(2) |
解:由题意可设直线L的方程为y=k(x-1) 设A(x1,y1),B(x2,y2)由
(关于k2的取值范围用如下方法得到,类比给分.当直线与抛物线相切时,|k|最大,此时△=0,得k2=1,所以|k|£
1,当直线过点(-3, 由 由 ∴x0的取值范围是 |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
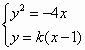 得,k2x2+(4-2k2)x+k2=0(8分)
得,k2x2+(4-2k2)x+k2=0(8分) ,解之得
,解之得 ,整理得,
,整理得,