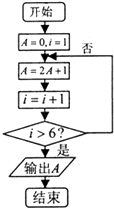
题目内容
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AB1⊥BC,且AA1=AB.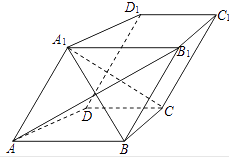
(1)求证:AB∥平面D1DCC1;
(2)求证:AB1⊥平面A1BC.
【答案】
(1)解:∵AB∥CD,CD平面D1DCC1,AB平面D1DCC1;
∴AB∥平面D1DCC1;
(2)解:在四棱柱ABCD﹣A1B1C1D1中,四边形ABB1A1为平行四边形,
∵AA1=AB,∴四边形ABB1A1为菱形,∴AB1⊥A1B,
∵AB1⊥BC,A1B∩BC=B,
∴AB1⊥平面A1BC,
【解析】1、由线线平行得到线面平行。
2、根据题意可知四边形ABB1A1为菱形,进而得到对角线互相垂直,再由已知根据线面垂直的判定定理可得证。
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】随着雾霾日益严重,很多地区都实行了“限行”政策,现从某地区居民中,随机抽取了300名居民了解他们对这一政策的态度,绘成如图所示的2×2列联表:
反对 | 支持 | 合计 | |
男性 | 70 | 60 | |
女性 | 50 | 120 | |
合计 |
(1)试问有没有99%的把握认为对“限行”政策的态度与性别有关?
(2)用样本估计总体,把频率作为概率,若从该地区所有的居民(人数很多)中随机抽取3人,用ξ表示所选3人中反对的人数,试写出ξ的分布列,并求出ξ的数学期望.
K2= ![]() ,其中n=a+b+c+d独立性检验临界表:
,其中n=a+b+c+d独立性检验临界表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |