Question

设椭圆中心在坐标原点，是它的两个顶点，直线与AB相交于点D，与椭圆相交于E、F两点。

（Ⅰ）若，求k的值；

（Ⅱ）求四边形AEBF面积的最大值。

Answer 1

解：（Ⅰ）依题设得椭圆的方程为

直线AB、EF的方程为

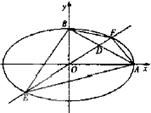
如图，设，其中，且x₁、x₂满足方程

故           ①

由知，得

由D在AB上知，得

所以

化简得 

解得      

（Ⅱ）解法一：根据点到直线的距离公式和①式知，点E、F到AB的距离分别为

  

   

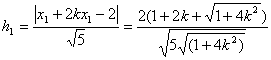
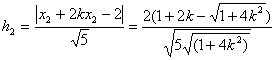
又所以四边形AEBF的面积为

  

    

   

   

     

当，即时，上式取等号，所以S的最大值为

解法二：由题设，

设，，由①得

故四边形AEBF的面积为

  

               

    

    

                     

当时，上式取等号，所以S的最大值为。