题目内容
设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.(Ⅰ)若
| ED |
| DF |
(Ⅱ)求四边形AEBF面积的最大值.
分析:(1)依题可得椭圆的方程,设直线AB,EF的方程分别为x+2y=2,y=kx,D(x0,kx0),E(x1,kx1),F(x2,kx2),且x1,x2满足方程(1+4k2)x2=4,进而求得x2的表达式,进而根据
=6
求得x0的表达式,由D在AB上知x0+2kx0=2,进而求得x0的另一个表达式,两个表达式相等求得k.
(Ⅱ)由题设可知|BO|和|AO|的值,设y1=kx1,y2=kx2,进而可表示出四边形AEBF的面积进而根据基本不等式的性质求得最大值.
| ED |
| DF |
(Ⅱ)由题设可知|BO|和|AO|的值,设y1=kx1,y2=kx2,进而可表示出四边形AEBF的面积进而根据基本不等式的性质求得最大值.
解答:解:(Ⅰ)依题设得椭圆的方程为
+y2=1,
直线AB,EF的方程分别为x+2y=2,y=kx(k>0).
如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,
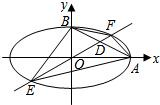
且x1,x2满足方程(1+4k2)x2=4,
故x2=-x1=
.①
由
=6
知x0-x1=6(x2-x0),得x0=
(6x2+x1)=
x2=
;
由D在AB上知x0+2kx0=2,得x0=
.
所以
=
,
化简得24k2-25k+6=0,
解得k=
或k=
.
(Ⅱ)由题设,|BO|=1,|AO|=2.由(Ⅰ)知,E(x1,kx1),F(x2,kx2),
不妨设y1=kx1,y2=kx2,由①得x2>0,根据E与F关于原点对称可知y2=-y1>0,
故四边形AEBF的面积为S=S△OBE+S△OBF+S△OAE+S△OAF
=
|OB|•(-x1)+
|OB|•x2+
|OA|•y2+
|OA|•(-y1)
=
|OB|(x2-x1)+
|OA|(y2-y1)
=x2+2y2
=
=
≤
=2
,
当x2=2y2时,上式取等号.所以S的最大值为2
.
| x2 |
| 4 |
直线AB,EF的方程分别为x+2y=2,y=kx(k>0).
如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x1<x2,

且x1,x2满足方程(1+4k2)x2=4,
故x2=-x1=
| 2 | ||
|
由
| ED |
| DF |
| 1 |
| 7 |
| 5 |
| 7 |
| 10 | ||
7
|
由D在AB上知x0+2kx0=2,得x0=
| 2 |
| 1+2k |
所以
| 2 |
| 1+2k |
| 10 | ||
7
|
化简得24k2-25k+6=0,
解得k=
| 2 |
| 3 |
| 3 |
| 8 |
(Ⅱ)由题设,|BO|=1,|AO|=2.由(Ⅰ)知,E(x1,kx1),F(x2,kx2),
不妨设y1=kx1,y2=kx2,由①得x2>0,根据E与F关于原点对称可知y2=-y1>0,
故四边形AEBF的面积为S=S△OBE+S△OBF+S△OAE+S△OAF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=x2+2y2
=
| (x2+2y2)2 |
|
2(
|
| 2 |
当x2=2y2时,上式取等号.所以S的最大值为2
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线的综合问题是支撑圆锥曲线知识体系的重点内容,问题的解决具有入口宽、方法灵活多样等,而不同的解题途径其运算量繁简差别很大.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
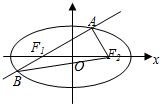 设椭圆中心在坐标原点,焦点在x轴上,一个顶点为
设椭圆中心在坐标原点,焦点在x轴上,一个顶点为