题目内容
如图所示，直角△ABC所在平面外一点S，且SA=SB=SC．
(1)求证：点S与斜边AC中点D的连线SD⊥面ABC；
(2)若直角边BA=BC，求证：BD⊥面SAC．
答案：
解析：
解析：
证明：由等腰三角形底边上的中线得到线线垂直，从而得到线面垂直． (1)在等腰△SAC中，D为AC中点，∴ SD⊥AC如图所示，取AB中点E，连DE、SE ∵ ED∥BC，BC⊥AB，∴ DE⊥AB 又SE⊥AB，∴ AB⊥面SED，∴ AB⊥SD ∴ SD⊥面ABC(AB、AC是面ABC内两相交直线) (2)∵ BA=BC，BD⊥AC 又∵ SD⊥面ABC，∴ SD⊥BD ∵ SD∩AC=D，∴ BD⊥面SAC
|
练习册系列答案
阅读快车系列答案
相关题目
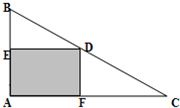Rt△ABC如图所示，直角边|AB|=3，|AC|=4．D点是斜边BC上的动点，DE⊥AB交于点E，DF⊥AC交于点F．设|AE|=x，四边形FDEA的面积为y，求y关于x的函数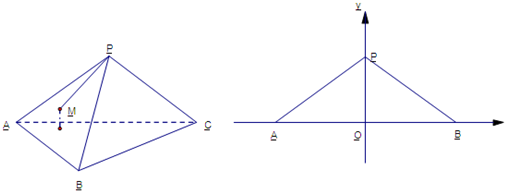
某小区规划一块周长为2a（a为正常数）的矩形停车场，其中如图所示的直角三角形ADP内为绿化区域．且∠PAC=∠CAB．设矩形的长AB=x，AB＞AD
有一矩形钢板ABCD缺损了一角（图中阴影部分），边缘线OM上每一点到点D的距离都等于它到边AB的距离．工人师傅要将缺损的一角切割下来使剩余部分成一个五边形，已知AB=4米，AD=2米．
（2013•永州一模）如图所示，直角梯形ABCD中，∠A=∠D=90°，AD=2，AB=3，CD=4，P在线段AB上，BP=1，O在CD上，且OP∥AD，将图甲沿OP折叠使得平面OCBP⊥底面ADOP，得到一个多面体（如图乙），M、N分别是AC、OP的中点．