题目内容
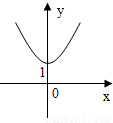
设a>1,实数x,y满足|x|-loga
=0,则y关于x的函数的图象形状大致是( )

| 1 | y |

分析:易求得y关于x的函数表达式,进而化为分段函数,由单调性及值域可作出判断.
解答:解:由|x|-loga
=0,得
=a|x|,
∴y=
=
,
又a>1,∴函数在(-∞,0]上递增,在(0,+∞)上递减,且y≤1,
故选B.
| 1 |
| y |
| 1 |
| y |
∴y=
| 1 |
| a|x| |
|
又a>1,∴函数在(-∞,0]上递增,在(0,+∞)上递减,且y≤1,
故选B.
点评:本题考查对数函数的图象与性质,属基础题,本题的关键是求得函数解析式.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
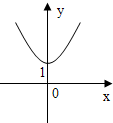
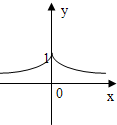
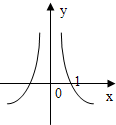
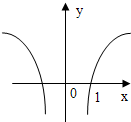

 =0,则y关于x的函数的图象形状大致是( )
=0,则y关于x的函数的图象形状大致是( )