题目内容
【题目】某企业从某种型号的产品中抽取了
件对该产品的某项指标
的数值进行检测，将其整理成如图所示的频率分布直方图，已知数值在100~110的产品有2l件.
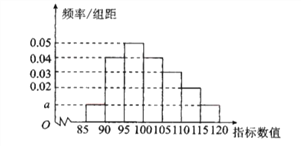
（1）求
和
的值；
（2）规定产品的级别如下表：
已知一件
级产品的利润分别为10，20，40元,以频率估计概率，现质检部门从该批产品中随机抽取两件，两件产品的利润之和为
，求
的分布列和数学期望；
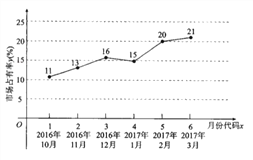
（3）为了了解该型号产品的销售状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图，由折线图可以看出，可用线性回归模型拟合月度市场卢有率
（%）与月份代码
之间的关系.求
关于
的线性回归方程，并预测2017年4月份(即
时)的市场占有率.
(参考公式：回归直线方程为
，其中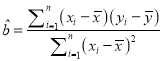
， 
【答案】(1) 
(2)见解析（3）2017年4月份的市场占有率预计为
【解析】试题分析：（1）第（1）问，根据频率公式求N,利用频率分布直方图的矩形的面积和为1求a. (2)第（2）问，先写出X的值，再列出分布列和求X的数学期望. (3)第（3）问，先利用最小二乘法求
关于
的线性回归方程
，再预测2017年4月份(即
时)的市场占有率.
试题解析：
（1）数值在100~110内的频率为
，所以
.
又因为
，所以
.
（2）由频率分布直方图，可知抽取的一件产品为
， 
， 
等级的概率分别为
， 
， 
，且
的取值为20，30，40，50，60，80，则
， 
， 
， 
， 
， 
，
所以
的分布列为
X | 20 | 30 | 40 | 50 | 60 | 80 |
P |
|
|
|
|
|
|
所以
.
（3）由折线图中所给的数据计算，
可得
， 
，
所以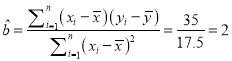
，
所以
，
故月度市场占有率
与月份序号
之间的线性回归方程为
.
当
时， 
.
所以2017年4月份的市场占有率预计为
.
【题目】近几年出现各种食品问题，食品添加剂会引起血脂增高、血压增高、血糖增高等疾病．为了解三高疾病是否与性别有关，医院随机对入院的60人进行了问卷调查，得到了如下的列联表：
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
（1）请将如图的列联表补充完整；若用分层抽样的方法在患三高疾病的人群中抽
人，其中女性抽多少人？
（2）为了研究三高疾病是否与性别有关，请计算出统计量
，并说明你有多大的把握认为三高疾病与性别有关？
下面的临界值表供参考：
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
（参考公式
，其中
）
【题目】铁人中学高二学年某学生对其亲属30人
饮食习惯进行了一次调查，并用如图所示的茎叶图表示30人的饮食指数．（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主．）
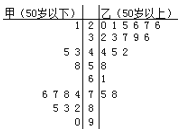
（Ⅰ）根据茎叶图，帮助这位学生说明其亲属30人的饮食习惯；
（Ⅱ）根据以上数据完成下列
的列联表：
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
（Ⅲ）能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系？
附：
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
