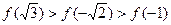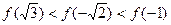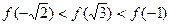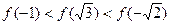题目内容
(本小题满分14分)
已知实系数一元二次方程x2+px+q=0的两根分别为x1,x2。
(1)若上述方程的一个根x1=4-i(i为虚数单位),求实数p,q的值;
(2)若方程的两根满足|x1|+|x2|=2,求实数p的取值范围。
已知实系数一元二次方程x2+px+q=0的两根分别为x1,x2。
(1)若上述方程的一个根x1=4-i(i为虚数单位),求实数p,q的值;
(2)若方程的两根满足|x1|+|x2|=2,求实数p的取值范围。
解:(1)根据“实系数方程虚根共 轭成对出现”,知x2=4+i, ……2分
轭成对出现”,知x2=4+i, ……2分
根据韦达定理,知p=-(x1+x2)=-8;q=x1·x2=17。 ……2分
(2)①当△=p2-4q<0时,方程的两根为虚数,且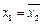 ,
,
∴|x1|=|x2|=1,∴q=1。∴p=-(x1+x2)=-2Re(x1)∈[-2,2],
又根据△=p2-4q<0,∴p∈(-2,2)。 ……3分
……3分
②(法一)当△=p2-4q≥0时,方程的两根为实数,
(2-1)当q>0时,方程的两根同号,∴|x1| +|x2|=|x1+x2|=|p|=2,∴p=±2;
+|x2|=|x1+x2|=|p|=2,∴p=±2;
(2-2)当q=0时,方程的一根为0,∴|x1|+|x2|=|x1+x2|=|p|=2,∴p=±2;
(2-2)当q<0时,方程的两根异号,∴|x1|+|x2|=|x1-x2|=2,
∴4=(x1+x2)2-4x1x2=p2-4q,∴p2=4+4q∈[0,4),∴p∈(-2,2)
∴当△≥0时,p∈[-2,2]。 ……3分
综上,p的取值范围是[-2,2]。
(法二)当△=p2-4q≥0时,方程的两根为实数,
∴|p|=|x1+x2|≤|x1|+|x2|=2,当x1与x2同号或有一个为0时等号取到。特别的,取x1=2,x2=0时p=-2;取x1 =-2,x2=0时p=2。
=-2,x2=0时p=2。
∴p∈[-2,2]。 ……3分
综上,p的取值范围是[-2,2]
 轭成对出现”,知x2=4+i, ……2分
轭成对出现”,知x2=4+i, ……2分根据韦达定理,知p=-(x1+x2)=-8;q=x1·x2=17。 ……2分
(2)①当△=p2-4q<0时,方程的两根为虚数,且
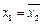 ,
,∴|x1|=|x2|=1,∴q=1。∴p=-(x1+x2)=-2Re(x1)∈[-2,2],
又根据△=p2-4q<0,∴p∈(-2,2)。
 ……3分
……3分②(法一)当△=p2-4q≥0时,方程的两根为实数,
(2-1)当q>0时,方程的两根同号,∴|x1|
 +|x2|=|x1+x2|=|p|=2,∴p=±2;
+|x2|=|x1+x2|=|p|=2,∴p=±2;(2-2)当q=0时,方程的一根为0,∴|x1|+|x2|=|x1+x2|=|p|=2,∴p=±2;
(2-2)当q<0时,方程的两根异号,∴|x1|+|x2|=|x1-x2|=2,
∴4=(x1+x2)2-4x1x2=p2-4q,∴p2=4+4q∈[0,4),∴p∈(-2,2)
∴当△≥0时,p∈[-2,2]。 ……3分
综上,p的取值范围是[-2,2]。
(法二)当△=p2-4q≥0时,方程的两根为实数,
∴|p|=|x1+x2|≤|x1|+|x2|=2,当x1与x2同号或有一个为0时等号取到。特别的,取x1=2,x2=0时p=-2;取x1
 =-2,x2=0时p=2。
=-2,x2=0时p=2。∴p∈[-2,2]。 ……3分
综上,p的取值范围是[-2,2]
略

练习册系列答案
相关题目
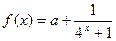 是奇函数.
是奇函数.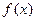 的单调性(不需要写出理由);
的单调性(不需要写出理由);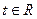 ,不等式
,不等式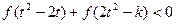 恒成立,求
恒成立,求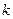 的取
的取 值范
值范 围.
围.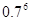 ,
,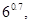
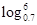 的大小关系为( )
的大小关系为( )
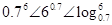
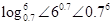
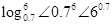
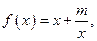 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在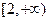 上的单调性?并证明你的结论.
上的单调性?并证明你的结论. 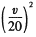 km,则这批货物全部运到B市最快需要________h,此时货车的速度是________km/h.
km,则这批货物全部运到B市最快需要________h,此时货车的速度是________km/h.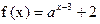 恒过定点
恒过定点  ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )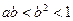
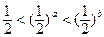
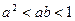

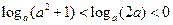 ,则
,则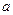 的取值范围是 。
的取值范围是 。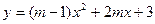 是偶函数,则
是偶函数,则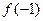 ,
,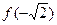 ,
,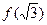 的大小关系为( )
的大小关系为( )