题目内容
(1)已知x<(2)已知x>0,y>0,且![]() +
+![]() =1,求x+y的最小值.
=1,求x+y的最小值.
解:(1)∵x<![]() ,∴5-4x>0.∴y=4x-2+
,∴5-4x>0.∴y=4x-2+![]() =-(5-4x+
=-(5-4x+![]() )+3≤-2+3=1.
)+3≤-2+3=1.
当且仅当5-4x=![]() ,即x=1时,上式等号成立.
,即x=1时,上式等号成立.
故当x=1时,ymax=1.
(2)∵x>0,y>0,![]() +
+![]() =1,
=1,
∴x+y=(![]() +
+![]() )(x+y)=
)(x+y)=![]() +
+![]() +10≥6+10=16.
+10≥6+10=16.
当且仅当![]() =
=![]() ,又
,又![]() +
+![]() =1,
=1,
即x=4,y=12时,上式等号成立.
故当x=4,y=12时,(x+y)min=16.

练习册系列答案
相关题目
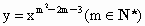 的图象关于y轴对称,且在(0,+∞)上函数值随x的增大而减小,求满足
的图象关于y轴对称,且在(0,+∞)上函数值随x的增大而减小,求满足 的a的范围.
的a的范围.
 ,xÎ(0,+∞).若
,xÎ(0,+∞).若 ,
, ,判断
,判断 与
与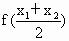 的大小,并加以证明.
的大小,并加以证明.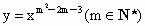 的图象关于y轴对称,且在(0,+∞)上函数值随x的增大而减小,求满足
的图象关于y轴对称,且在(0,+∞)上函数值随x的增大而减小,求满足 的a的范围.
的a的范围. ,xÎ(0,+∞).若
,xÎ(0,+∞).若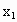 ,
, ,判断
,判断 与
与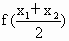 的大小,并加以证明.
的大小,并加以证明.