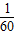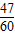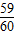题目内容
3人独立地破译一个密码,每人破译出密码的概率分别是
、
、
,则此密码被破译出的概率是( )
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
分析:记密码被破译出为事件A,则
为密码没有被破译出,即三人都不能译出密码,根据题意易得三人不能译出的概率,进而可得P(
),由对立事件的性质,计算可得答案.
. |
| A |
. |
| A |
解答:解:记密码被破译出为事件A,则其对立事件
为密码没有被破译出,即三人都不能译出密码
根据题意,三人不能译出的概率分别为1-
、1-
、1-
,
则P(
)=(1-
)(1-
)(1-
)=
,
故则该密码被破译的概率P(A)=1-
=
,
故选D.
. |
| A |
根据题意,三人不能译出的概率分别为1-
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
则P(
. |
| A |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 2 |
| 5 |
故则该密码被破译的概率P(A)=1-
| 2 |
| 5 |
| 3 |
| 5 |
故选D.
点评:本题考查相互独立事件的概率计算,注意利用对立事件的性质,可以避免分类讨论,简化计算.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 、
、 、
、 ,则此密码被破译出的概率是
,则此密码被破译出的概率是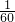
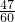
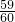

 、
、 、
、 ,则此密码被破译出的概率是( )
,则此密码被破译出的概率是( )