题目内容
点(3,1)和(-4,6)在直线3x-2y+a=0的两侧,则( )
| A.a<-7或a>24 | B.-7<a<24 |
| C.a=-7或a=24 | D.以上都不对 |
B
解析试题分析:因为点(3,1)和点(-4,6)在直线3x-2y+a=0的两侧,
所以,(3×3-2×1+a)[3×(-4)-2×6+a]<0,
即:(a+7)(a-24)<0,
解得-7<a<24
故选B.
考点:本题主要考查了二元一次不等式所表示的区域的运用。
点评:准确把握点与直线的位置关系,找到图中的“界”,是解决此类问题的关键。规律是:点在直线的同侧,代入后函数值同号,点在直线的一侧,代入后函数值异号。

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
不等式组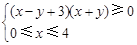 表示的平面区域是
表示的平面区域是
| A.矩形 | B.三角形 | C.直角梯形 | D.等腰梯形 |
已知实数 满足
满足 则
则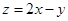 的最小值是( )
的最小值是( )
| A.7 | B.-5 | C.4 | D.-7 |
在平面直角坐标系中,若不等式组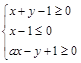 (
(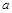 为常数)所表示的平面区域内的面积等于2,则
为常数)所表示的平面区域内的面积等于2,则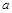 的值为( )
的值为( )
| A.-5 | B.1 | C.2 | D.3 |
满足线性约束条件 的目标函数
的目标函数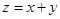 的最大值是( )
的最大值是( )
| A.1 | B.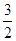 | C.2 | D.3 |
若整数 满足
满足 则
则 的最大值是 ( )
的最大值是 ( )
| A.1 | B.5 | C.2 | D.3 |
设变量 满足约束条件
满足约束条件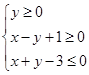 ,则
,则 的最大值为 ( )
的最大值为 ( )
| A.—2 | B.4 | C.6 | D.8 |
设 满足约束条件
满足约束条件 若目标函数
若目标函数 的最大值为
的最大值为 则
则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
已知实数 满足
满足 的最大值为( )
的最大值为( )
| A.—3 | B.—2 | C.1 | D.2 |