题目内容
一个棱锥被平行于底面的平面所截,若截面面积与底面面积之比为9:25,则此棱锥的侧棱被分成上下两部分之比为
3:2
3:2
.分析:根据棱锥的截面性质,知平行于底面的平面截棱锥所得的截面与底面相似,且相似比等于截得的小棱锥与原棱锥对应棱长之比.根据截面面积与底面面积之比可求出相似比,就可得到棱锥的侧棱被分成上下两部分之比.
解答:解:∵在棱锥中,平行于底面的平面截棱锥所得的截面与底面相似,
相似比等于截得的小棱锥与原棱锥对应棱长之比.
又∵截面面积与底面面积之比为9:25,∴相似比为3:5
即截得的小棱锥与原棱锥对应棱长之比为3:5
∴棱锥的侧棱被分成上下两部分之比为3:2
故答案为3:2
相似比等于截得的小棱锥与原棱锥对应棱长之比.
又∵截面面积与底面面积之比为9:25,∴相似比为3:5
即截得的小棱锥与原棱锥对应棱长之比为3:5
∴棱锥的侧棱被分成上下两部分之比为3:2
故答案为3:2
点评:本题主要考查了棱锥的截面性质定理,属于立体几何中的基础题.

练习册系列答案
相关题目
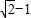 )
)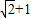 )
)