题目内容
已知椭圆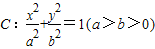 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.(Ⅰ)求椭圆的方程; (Ⅱ)过点Q(-1,0)的直线l交椭圆于A,B两点,交直线x=-4于点E,且
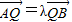 ,
,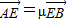 .求证:λ+μ为定值,并计算出该定值.
.求证:λ+μ为定值,并计算出该定值.
【答案】分析:(Ⅰ)由条件得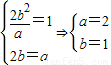 ,从而写出椭圆的方程即可;
,从而写出椭圆的方程即可;
(Ⅱ)易知直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的坐标公式即可求得λ+μ值,从而解决问题.
解答:解:(Ⅰ)由条件得 ,所以方程为
,所以方程为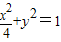
(Ⅱ)易知直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y)
由
△=48k2+16>0
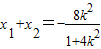 ,
,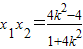
由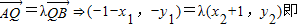
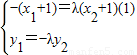
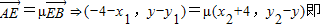
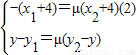
由(1)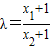 ,由(2)
,由(2)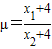
∴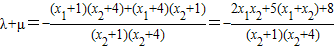
将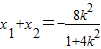 ,
,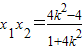 代入有∴
代入有∴
点评:本小题主要考查直线与圆锥曲线的综合问题、向量在几何中的应用等基础知识,考查运算求解能力,考查数形结合思想与转化思想.属于基础题.
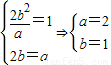 ,从而写出椭圆的方程即可;
,从而写出椭圆的方程即可;(Ⅱ)易知直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量的坐标公式即可求得λ+μ值,从而解决问题.
解答:解:(Ⅰ)由条件得
 ,所以方程为
,所以方程为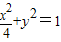
(Ⅱ)易知直线l斜率存在,令l:y=k(x+1),A(x1y1),B(x2,y2),E(-4,y)
由

△=48k2+16>0
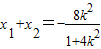 ,
,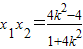
由
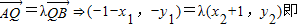
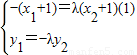
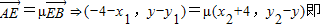
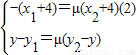
由(1)
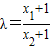 ,由(2)
,由(2)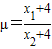
∴
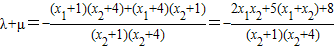
将
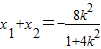 ,
,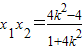 代入有∴
代入有∴
点评:本小题主要考查直线与圆锥曲线的综合问题、向量在几何中的应用等基础知识,考查运算求解能力,考查数形结合思想与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的离心率为
的离心率为 ,直线
,直线 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点
,右焦点 ,直线
,直线 过点
过点 垂
垂 ,线段
,线段 垂直平分线交
垂直平分线交 ,求点
,求点 的方程;
的方程; 轴上时,在曲线
轴上时,在曲线