题目内容
已知向量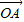 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0), =(-sinβ,cosβ
=(-sinβ,cosβ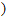 .其中O为坐标原点.
.其中O为坐标原点.(I)若
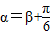 且m>0,求向量
且m>0,求向量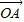 与
与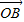 的夹角;
的夹角;(II)当实数α,β变化时,求实数
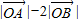 的最大值.
的最大值.
【答案】分析:(Ⅰ)设它们的夹角为θ,利用向量的数量积公式表示出cosθ,将已知条件 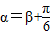 代入,利用特殊角的三角函数值求出两个向量的夹角.
代入,利用特殊角的三角函数值求出两个向量的夹角.
(II)先将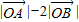 利用向量模的计算公式表示成
利用向量模的计算公式表示成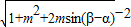 ,再利用三角函数的值域求出它的最大值即可.
,再利用三角函数的值域求出它的最大值即可.
解答:解:(I)设它们的夹角为θ,则:

=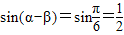 ,
,
故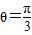 …(6分)
…(6分)
(II)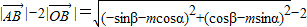
=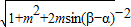 …(10分)
…(10分)
所以当m>0时,原式的最大值是m-1;
当m<0时,原式的最大值是-m-1…(12分)
点评:求向量的夹角问题,一般利用向量的数量积公式来解决;解决向量的模的最值问题,一般转化为函数的最值来解决.
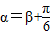 代入,利用特殊角的三角函数值求出两个向量的夹角.
代入,利用特殊角的三角函数值求出两个向量的夹角.(II)先将
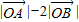 利用向量模的计算公式表示成
利用向量模的计算公式表示成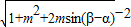 ,再利用三角函数的值域求出它的最大值即可.
,再利用三角函数的值域求出它的最大值即可.解答:解:(I)设它们的夹角为θ,则:

=
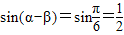 ,
,故
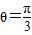 …(6分)
…(6分)(II)
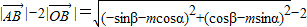
=
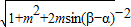 …(10分)
…(10分)所以当m>0时,原式的最大值是m-1;
当m<0时,原式的最大值是-m-1…(12分)
点评:求向量的夹角问题,一般利用向量的数量积公式来解决;解决向量的模的最值问题,一般转化为函数的最值来解决.

练习册系列答案
相关题目
 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),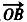 =(-sinβ,cosβ),其中O为坐标原点。
=(-sinβ,cosβ),其中O为坐标原点。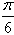 且m>0,求向量
且m>0,求向量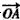 与
与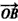 的夹角;
的夹角;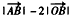 的最大值。
的最大值。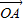 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),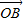 =(-sinβ,cosβ
=(-sinβ,cosβ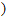 .其中O为坐标原点.
.其中O为坐标原点.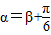 且m>0,求向量
且m>0,求向量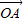 与
与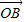 的夹角;
的夹角;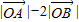 的最大值.
的最大值.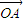 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),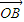 =(-sinβ,cosβ
=(-sinβ,cosβ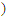 .其中O为坐标原点.
.其中O为坐标原点.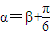 且m>0,求向量
且m>0,求向量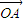 与
与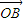 的夹角;
的夹角;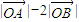 的最大值.
的最大值.