题目内容
已知向量 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),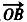 =(-sinβ,cosβ),其中O为坐标原点。
=(-sinβ,cosβ),其中O为坐标原点。
(1)若α=β+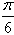 且m>0,求向量
且m>0,求向量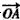 与
与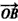 的夹角;
的夹角;
(2)当实数α、β变化时,求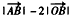 的最大值。
的最大值。
 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),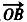 =(-sinβ,cosβ),其中O为坐标原点。
=(-sinβ,cosβ),其中O为坐标原点。(1)若α=β+
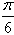 且m>0,求向量
且m>0,求向量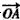 与
与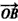 的夹角;
的夹角;(2)当实数α、β变化时,求
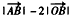 的最大值。
的最大值。解:(1)设向量 与
与 的夹角为θ(θ∈[0,π]),
的夹角为θ(θ∈[0,π]),
则

又∵
∴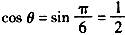
故
即向量 与
与 的夹角为
的夹角为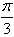 。
。
(2)由题意得

则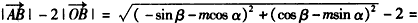
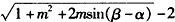
所以当m>0时,原式的最大值是m-1;
当m<0时,原式的最大值是-m-1。
 与
与 的夹角为θ(θ∈[0,π]),
的夹角为θ(θ∈[0,π]),则


又∵

∴
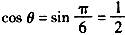
故

即向量
 与
与 的夹角为
的夹角为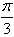 。
。(2)由题意得

则
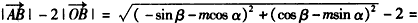
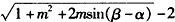
所以当m>0时,原式的最大值是m-1;
当m<0时,原式的最大值是-m-1。

练习册系列答案
相关题目
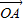 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),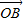 =(-sinβ,cosβ
=(-sinβ,cosβ .其中O为坐标原点.
.其中O为坐标原点.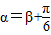 且m>0,求向量
且m>0,求向量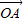 与
与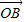 的夹角;
的夹角;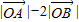 的最大值.
的最大值.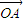 =(mcosα,msinα)(m≠0),
=(mcosα,msinα)(m≠0),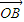 =(-sinβ,cosβ
=(-sinβ,cosβ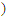 .其中O为坐标原点.
.其中O为坐标原点.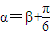 且m>0,求向量
且m>0,求向量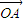 与
与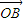 的夹角;
的夹角;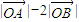 的最大值.
的最大值.