题目内容
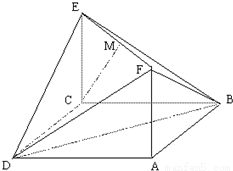
 (文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,AB=
(文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,AB=| 2 |
AF=1,M是线段EF的中点.
(1)求异面直线CM与直线AB所成的角的大小;
(2)求多面体EFABCD的表面积.
分析:(1)连接MD,可通过面面垂直得到线面垂直,从而在直角三角形中用勾股定理算出DC=CM=DM,得到△CDM是等边三角形.而根据CD∥AB,可得∠CDM即为异面直线CM与AB所成的角,得到CM与直线AB所成的角为60°;
(2)多面体EFABCD的表面积为四个全等的直角三角形,加上两个全等的等腰三角形和一个正方形,根据(1)的计算和证明的结论,得到这个表面积.
(2)多面体EFABCD的表面积为四个全等的直角三角形,加上两个全等的等腰三角形和一个正方形,根据(1)的计算和证明的结论,得到这个表面积.
解答:解:(1)∵CD∥AB,∴∠CDM(或其补角)即为异面直线CM与AB所成的角,…(2分)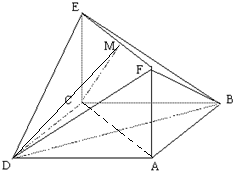
连接MD,在△CEM中,CE=EM=1,CE⊥EM
∴CM=
CM=CE2+EM2=2,
∵平面ACEF⊥平面ABCD,平面ACEF∩平面ABCD=AC,CE⊥AC
∴CE⊥平面ABCD,结合CD?平面ABCD,得CE⊥CD
又∵Rt△CDE中,DE=
=
,同理DF=
,∴DE=DF,
∵M是线段EF的中点,∴DM=
=
,
∴△CDM中,DC=CM=DM=
,△CDM是等边三角形,…(5分)
所以∠CMD=60°,即异面直线CM与AB所成的角为60°;…(6分)
(2)由(1)的计算,得S△CDE=S△BCE=S△ADF=S△ABF=
•
•1=
,…(8分)
S△BEF=S△DEF=
•2•
=
…(10分)
而SABCD=(
)2=2
∴多面体EFABCD的表面积为:S表=4S△ABF+2S△DEF+SABCD=4
+2.…(12分)

连接MD,在△CEM中,CE=EM=1,CE⊥EM
∴CM=
| 2 |
∵平面ACEF⊥平面ABCD,平面ACEF∩平面ABCD=AC,CE⊥AC
∴CE⊥平面ABCD,结合CD?平面ABCD,得CE⊥CD
又∵Rt△CDE中,DE=
| CE2+CD 2 |
| 3 |
| 3 |
∵M是线段EF的中点,∴DM=
| DF2-MF2 |
| 2 |
∴△CDM中,DC=CM=DM=
| 2 |
所以∠CMD=60°,即异面直线CM与AB所成的角为60°;…(6分)
(2)由(1)的计算,得S△CDE=S△BCE=S△ADF=S△ABF=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
S△BEF=S△DEF=
| 1 |
| 2 |
| 2 |
| 2 |
而SABCD=(
| 2 |
∴多面体EFABCD的表面积为:S表=4S△ABF+2S△DEF+SABCD=4
| 2 |
点评:本题给出一个特殊的多面体,叫我们求异面直线所成角和几何体的表面积,着重考查了线面垂直与面面垂直的判定与性质和异面直线所成角的求法等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

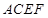 的边
的边 与正方形
与正方形 所在平面垂直,
所在平面垂直, ,
,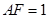 ,
,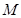 是线段
是线段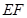 的中点。
的中点。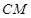 与直线
与直线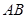 所成的角的大小;
所成的角的大小; 的表面积。
的表面积。
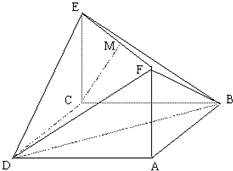 (文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,
(文)如图,已知矩形ACEF的边CE与正方形ABCD所在平面垂直,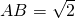 ,
,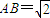 ,
,