Question

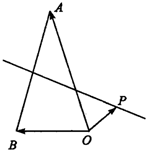
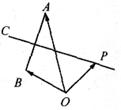
设O、A、B是平面内不共线的三点，记

OA

=

a

， 

OB

=

b

，若P为线段AB垂直平分线上任意一点，且

OP

=

p

，当|

a

|=2，|

b

|=1时，则

p

•(

a

-

b)

等于（　　）

• A．3
• B．0
• C．

  5

  2

• D．

  3

  2

Answer 1

分析：设M是AB的中点，将向量

OP

表示成

OM

+

MP

，而

OA

-

OB

=

BA

，从而

OP

•(

OA

-

OB

)=

OM

•

BA

+

MP

•

BA

，再结合P为线段AB垂直平分线上任意一点，得

MP

•

BA

=0，转化为求数量积

OM

•

BA

，再用

OM

=

1

2

(

OA

+

OB

)，

OA

-

OB

=

BA

代入，得

OP

•(

OA

-

OB

)=

1

2

(|

OA

| 2-|

OB

| 2)，结合已知条件的数据，不难得出这个数量积．

解答：解：设M是线段AB的中点，根据题意，得

OP

=

OM

+

MP

，

OA

-

OB

=

BA

∴

OP

•(

OA

-

OB

)=(

OM

+

MP

)•

BA

=

OM

•

BA

+

MP

•

BA

∵

MP

与

BA

互相垂直
∴

MP

•

BA

=0
因此

OP

•(

OA

-

OB

)=

OM

•

BA

又∵△OAB中，OM是AB边上的中线
∴

OM

=

1

2

(

OA

+

OB

)
∴

OM

•

BA

=

1

2

(

OA

+

OB

) •

BA

=

1

2

(

OA

+

OB

)(

OA

-

OB

)
即

OM

•

BA

=

1

2

(|

OA

| 2-|

OB

| 2)
∵|

OA

|=2，|

OB

|=1，
∴

OP

•(

OA

-

OB

)=

OM

•

BA

=

1

2

(22-12)=

3

2

故选D．

点评：本题考查了平面向量数量积的运算，着重考查了数量积在三角形中的应用，考查转化思想，计算能力，是中档题．