Question

（2010•江苏模拟）设实数x，y满足

x-y-2≤0 x+2y-5≥0 y-2≤0

则u=

y2-x2

xy

的取值范围是

[-

8

3

，

3

2

]

．

Answer 1

分析：先根据根的分布列出约束条件画出可行域，再化简u=

y

x

-

1

y x

，设z'=

y

x

最后利用几何意义求最值，本例中

y

x

的取值的几何意义是斜率．

解答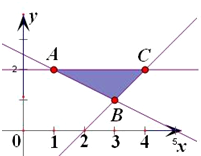：解：作出可行域，如图
u=

y

x

-

1

y x

，设z'=

y

x

，
当把z'看作常数时，它表示直线y=z'x的斜率，
因此，当直线y=z'x过点A时，z最大；
当直线y=z'x过点B时，z最小．
由y=2，x+2y-5=0，得A（1，2）．
由x+2y-5=0，x-y-2=0，得B（3，1）．
∴z'_max=2，z_min=

1

3

．
故z'的取值范围是[

1

3

，2]．
∴u=

y

x

-

1

y x

是关于z'=

y

x

单调增函数，它的取值范围为[-

8

3

，

3

2

]．
故答案为：[-

8

3

，

3

2

]．

点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于中档题．