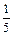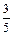题目内容
已知函数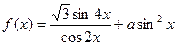 在
在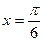 时取到最大值.
时取到最大值.
(1)求函数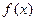 的定义域;
的定义域;
(2)求实数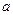 的值.
的值.
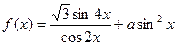 在
在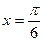 时取到最大值.
时取到最大值.(1)求函数
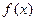 的定义域;
的定义域;(2)求实数
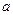 的值.
的值.(1){x|x≠kπ+, (k∈Z)} (2) a=-4
(1) x要满足cos2x≠0, 从而2x≠kπ+ (k∈Z)
因此f(x)的定义域为{x|x≠kπ+, (k∈Z)} ----------(2分)
(2)由f(x)=" f(x)=" +asin2x=2sin2x+(1-cos2x)
∴f(x)= 2sin2x-cos2x+≤ + -----------(6分)
∵x=时, f(x)取到最大值, 则2sin-cos =

∴ 3- =
 , 求得a=-4
, 求得a=-4因此所求实数a的值为-4 --------------(10分)

练习册系列答案
相关题目
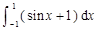 的值为
的值为
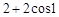

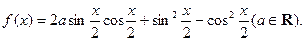
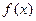 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;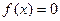 的条件下,求
的条件下,求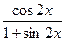 的值.
的值.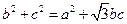 ,求:
,求: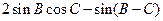 的值。
的值。 ,其中向量
,其中向量 ,
, ,
, ,
, 的单调递减区间及对称轴方程;
的单调递减区间及对称轴方程; 成立的
成立的 的取值范围.
的取值范围.
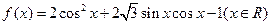
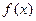 的周期、对称轴方程;(2)求函数
的周期、对称轴方程;(2)求函数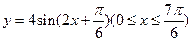 的图象与一条平行于x轴的直线有三个交点,其横坐标分别为
的图象与一条平行于x轴的直线有三个交点,其横坐标分别为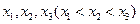 ,则
,则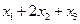 =
= 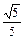 ,则sin4α-cos4α的值为( )
,则sin4α-cos4α的值为( )