题目内容
定义在R上的函数 的值
的值
为( )
 的值
的值为( )
| A.2 | B.0 | C.—1 | D.1 |
C
通过对x>0时函数值的关系,仿写新的等式,判断出函数以6为周期,将f(2011)转化为f(1)的值代入解析式求出值.
解:当x>0时,f(x)=f(x-1)-f(x-2);
所以有f(x-1)=f(x-2)-f(x-3);
所以f(x)=-f(x-3);所以f(x)=f(x-6);
所以f(x)的周期为6;
所以f(2011)=f(335×6+1)=f(1)=f(0)-f(-1)=-1;
故答案为C.
解:当x>0时,f(x)=f(x-1)-f(x-2);
所以有f(x-1)=f(x-2)-f(x-3);
所以f(x)=-f(x-3);所以f(x)=f(x-6);
所以f(x)的周期为6;
所以f(2011)=f(335×6+1)=f(1)=f(0)-f(-1)=-1;
故答案为C.

练习册系列答案
相关题目
 .
. 的图象;
的图象; 
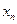 表示某鱼群在第
表示某鱼群在第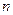 年初的总量,
年初的总量,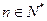 ,且
,且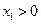 。不考虑其他因素,设在第
。不考虑其他因素,设在第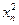 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数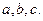 其中
其中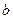 称为捕捞强度。
称为捕捞强度。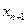 与
与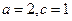 ,为了保证对任
,为了保证对任 意
意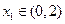 ,都有
,都有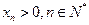 ,则捕捞强度
,则捕捞强度 的图像大致是( )
的图像大致是( )
 的一个根在(0,1)内,另一个根在(1,2)内,求:
的一个根在(0,1)内,另一个根在(1,2)内,求: 的取值范围;
的取值范围; 的取值范围;
的取值范围; 的取值范围.
的取值范围.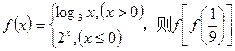 = 。
= 。
 ,函数
,函数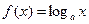 在区间
在区间 上的最大值与最小值之差为
上的最大值与最小值之差为 ,
, 的值为( )
的值为( )

 ,若
,若 ,则
,则