题目内容
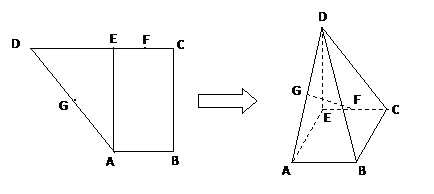
如图,已知直角梯形![]() 中,
中, ![]() 过
过![]()
作![]() ,垂足为
,垂足为![]() ,
,![]()
![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折叠,使得
折叠,使得![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)在线段![]() 上找一点
上找一点![]() ,使得面
,使得面![]() 面
面![]() ,并说明理由.
,并说明理由.
![]() ;
;![]() ;中点
;中点
解析:
(1)证明:由已知得:DE⊥AE,DE⊥EC,∴DE⊥面ABCE
∴DE⊥BC,又BC⊥CE,∴BC⊥面DCE
(2)证明:取AB中点H,连接GH,FH
∴GH‖BD, BD![]() 面BCD, GH
面BCD, GH![]() 面BCD
面BCD
∴GH‖面BCD
同理FH‖面BCD
∴面FHG‖面BCD ∴GF‖面BCD
(3)分析可知,R点满足3AR=RE时,面BDR⊥面BDC
证明:取BD中点Q,连结DR、BR、CR、CQ、RQ
![]() 容易计算CD=2,BD=,CR=,DR=
容易计算CD=2,BD=,CR=,DR=![]() ,CQ=
,CQ=![]()
在▲BDR中∵BR=,DR=![]() ,BD=
,BD=![]() ,可知RQ=
,可知RQ=
∴在▲CRQ中,CQ2+RQ2=CR2,∴CQ⊥RQ
又在▲CBD中,CD=CB,Q为BD中点∴CQ⊥BD.
∴CQ⊥面BDR,∴面BDC⊥面BDR

练习册系列答案
相关题目
 中,
中,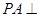 底面
底面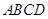 ,四边形
,四边形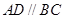 ,
,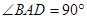 ,
,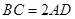 ,
,
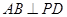 ;
;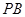 上找出一点
上找出一点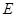 ,使
,使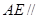 平面
平面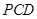 ,
,
