题目内容
设x1、x2∈R,规定运算“*”:x1*x2=(x1+x2)2+(x1-x2)2.(Ⅰ)若x≥0,a>0,求动点P(x,
 )的轨迹c;
)的轨迹c;(Ⅱ)设P(x,y)是平面内任意一点,定义:d1(p)=
 ,d2(p)=
,d2(p)= ,问在(Ⅰ)中的轨迹c上是否存在两点A1、A2,使之满足d1(Ai)=
,问在(Ⅰ)中的轨迹c上是否存在两点A1、A2,使之满足d1(Ai)= )(i=1、2),若存在,求出a的范围.
)(i=1、2),若存在,求出a的范围.
【答案】分析:(I)由题中“*”运算的定义,得动点P(x,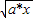 )满足
)满足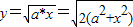 ,得y2=2(a2+x2),化简即得所求轨迹c是焦点在y轴上的双曲线,在第一象限内的一部分;
,得y2=2(a2+x2),化简即得所求轨迹c是焦点在y轴上的双曲线,在第一象限内的一部分;
(II)根据题意,化简得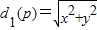 且d2(p)=|x-a|,假设存在两点A1、A2满足题设的条件,y2=2(a2+x2)消去y得关于x的一元二次方程:(3-a)x2+2a2x+2a2-a3=0,此方程有两个非负的实数根.由此结合根的判别式与韦达定理,建立关于a的不等式组并解之,即可得到实数a的取值范围.
且d2(p)=|x-a|,假设存在两点A1、A2满足题设的条件,y2=2(a2+x2)消去y得关于x的一元二次方程:(3-a)x2+2a2x+2a2-a3=0,此方程有两个非负的实数根.由此结合根的判别式与韦达定理,建立关于a的不等式组并解之,即可得到实数a的取值范围.
解答:解:(Ⅰ)∵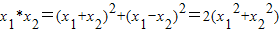
∴当x≥0时,设P(x,y),则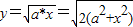 ,
,
∴y2=2(a2+x2)(y>0)化简得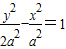 (x≥0,y>0),
(x≥0,y>0),
所求轨迹c是实半轴长为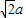 、虚半轴长为a,焦点在y轴上的双曲线,
、虚半轴长为a,焦点在y轴上的双曲线,
在第一象限内的一部分(包括上顶点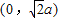 )…6′
)…6′
(Ⅱ)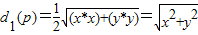 ,
,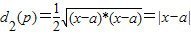 .
.
假设存在两点A1、A2,使得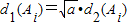 (i=1、2),即
(i=1、2),即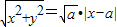 .
.
∴x2+y2=a•(x-a)2,
又∵y2=2(a2+x2),∴x2+2(a2+x2)=a•(x-a)2,
即(3-a)x2+2a2x+2a2-a3=0有两非负实数根.…10′
∴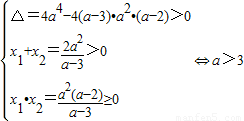
故当a>3时,存在适合条件的两点.…13′.
点评:本题给出新定义,求动点的轨迹方程并依此讨论满足指定条件的点的存在性.着重考查了一元二次方程根与系数的关系、根的判别式和圆锥曲线的定义与性质等知识,属于中档题.
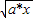 )满足
)满足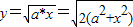 ,得y2=2(a2+x2),化简即得所求轨迹c是焦点在y轴上的双曲线,在第一象限内的一部分;
,得y2=2(a2+x2),化简即得所求轨迹c是焦点在y轴上的双曲线,在第一象限内的一部分;(II)根据题意,化简得
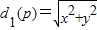 且d2(p)=|x-a|,假设存在两点A1、A2满足题设的条件,y2=2(a2+x2)消去y得关于x的一元二次方程:(3-a)x2+2a2x+2a2-a3=0,此方程有两个非负的实数根.由此结合根的判别式与韦达定理,建立关于a的不等式组并解之,即可得到实数a的取值范围.
且d2(p)=|x-a|,假设存在两点A1、A2满足题设的条件,y2=2(a2+x2)消去y得关于x的一元二次方程:(3-a)x2+2a2x+2a2-a3=0,此方程有两个非负的实数根.由此结合根的判别式与韦达定理,建立关于a的不等式组并解之,即可得到实数a的取值范围.解答:解:(Ⅰ)∵
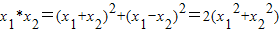
∴当x≥0时,设P(x,y),则
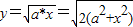 ,
,∴y2=2(a2+x2)(y>0)化简得
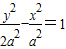 (x≥0,y>0),
(x≥0,y>0),所求轨迹c是实半轴长为
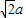 、虚半轴长为a,焦点在y轴上的双曲线,
、虚半轴长为a,焦点在y轴上的双曲线,在第一象限内的一部分(包括上顶点
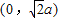 )…6′
)…6′(Ⅱ)
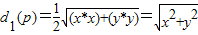 ,
,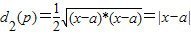 .
.假设存在两点A1、A2,使得
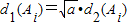 (i=1、2),即
(i=1、2),即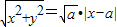 .
.∴x2+y2=a•(x-a)2,
又∵y2=2(a2+x2),∴x2+2(a2+x2)=a•(x-a)2,
即(3-a)x2+2a2x+2a2-a3=0有两非负实数根.…10′
∴
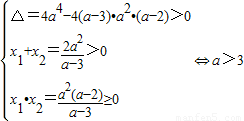
故当a>3时,存在适合条件的两点.…13′.
点评:本题给出新定义,求动点的轨迹方程并依此讨论满足指定条件的点的存在性.着重考查了一元二次方程根与系数的关系、根的判别式和圆锥曲线的定义与性质等知识,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 )的轨迹c;
)的轨迹c; ,d2(p)=
,d2(p)= ,问在(Ⅰ)中的轨迹c上是否存在两点A1、A2,使之满足d1(Ai)=
,问在(Ⅰ)中的轨迹c上是否存在两点A1、A2,使之满足d1(Ai)= )(i=1、2),若存在,求出a的范围.
)(i=1、2),若存在,求出a的范围.