题目内容
如果一个函数的导函数是f′（x）=
+
，则这个函数可能是（ ）
| 1 |
| xln2 |
| 1 |
| sin2x |
| A、f（x）=log2x-cotx |
| B、f（x）=log2x+cotx |
| C、f（x）=-log2x-cotx |
| D、f（x）=-log2x+cotx |
分析：因为当f（x）=log2x-cotx，利用商的导数运算法则及对数的导数公式求出f（x）的导数，即为
解答：解：当f（x）=log2x-cotx
=log2x-
所以f′(x)=
-
=
+
故选A
=log2x-
| cosx |
| sinx |
所以f′(x)=
| 1 |
| xln2 |
| -sinx•sinx-cosx•cosx |
| sin2x |
| 1 |
| xln2 |
| 1 |
| sin2x |
故选A
点评：解选择题常用的方法是排除法，这是一种有效的方法．是一道基础题．
练习册系列答案
相关题目
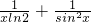，则这个函数可能是
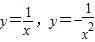，lnx六个函数的六张外形完全一致的卡片（一张卡片一个函数），参与者有放回的抽取卡片，参与者只参加一次．如果只抽一张，抽得卡片上的函数是其它某一张卡片上函数的导数，抽取者将获得三等奖；如是先后各抽一张，抽出的卡片中，其中一张上的函数是另一张卡片上函数的导数，抽取者将获得二等奖；如果先后各抽一张，第一张卡片上的函数的导数是第二张卡片上的函数，抽取者将获得一等奖．
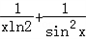，则这个函数可能是