题目内容
某校一次数学研究性学习活动中,一个密封的箱子内装有分别写上y=sinx,y=cosx,y=ex,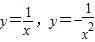 ,lnx六个函数的六张外形完全一致的卡片(一张卡片一个函数),参与者有放回的抽取卡片,参与者只参加一次.如果只抽一张,抽得卡片上的函数是其它某一张卡片上函数的导数,抽取者将获得三等奖;如是先后各抽一张,抽出的卡片中,其中一张上的函数是另一张卡片上函数的导数,抽取者将获得二等奖;如果先后各抽一张,第一张卡片上的函数的导数是第二张卡片上的函数,抽取者将获得一等奖.
,lnx六个函数的六张外形完全一致的卡片(一张卡片一个函数),参与者有放回的抽取卡片,参与者只参加一次.如果只抽一张,抽得卡片上的函数是其它某一张卡片上函数的导数,抽取者将获得三等奖;如是先后各抽一张,抽出的卡片中,其中一张上的函数是另一张卡片上函数的导数,抽取者将获得二等奖;如果先后各抽一张,第一张卡片上的函数的导数是第二张卡片上的函数,抽取者将获得一等奖.(Ⅰ)求学生甲抽一次获得三等奖的概率;
(Ⅱ)求学生乙抽一次获得二等奖的概率;
(Ⅲ)求学生丙抽一次获得一等奖的概率.
【答案】分析:(Ⅰ)在所给的六个函数中,有y=cosx,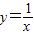 ,
,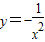 这三个函数可作为其它函数的导数,由此求得学生甲抽一次获得三等奖的概率.
这三个函数可作为其它函数的导数,由此求得学生甲抽一次获得三等奖的概率.
(Ⅱ)在六个函数的卡片中,先后抽两次,不同的抽法有36种.其中,有7种抽法满足得二等奖的要求,由此求得学生乙抽一次获得二等奖的概率.
(Ⅲ)在六个函数的卡片中,先后抽两次,不同的抽法有36种.其中,有4种抽法满足得一等奖的要求,由此求得学生丙抽一次获得一等奖的概率.
解答:解:(Ⅰ)在y=sinx,y=cosx,y=ex,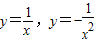 ,lnx六个函数中,y=cosx,
,lnx六个函数中,y=cosx,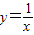 ,
,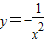 这三个函数可作为其它函数的导数.
这三个函数可作为其它函数的导数.
设“学生甲抽一次获得三等奖”为事件A,∴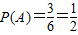 .…4分
.…4分
(Ⅱ)在y=sinx,y=cosx,y=ex,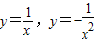 ,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种,
,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种,
其中,y=sinx,y=cosx组合两种,y=ex,y=ex组合一种,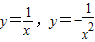 组合两种,lnx,
组合两种,lnx,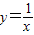 组合两种,共计7种都满足得二等奖的要求.
组合两种,共计7种都满足得二等奖的要求.
设“学生乙抽一次获得二等奖”为事件B,∴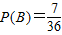 .…8分
.…8分
(Ⅲ)在y=sinx,y=cosx,y=ex,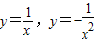 ,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种.
,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种.
其中,y=sinx,y=cosx组合1种,y=ex,y=ex组合1种,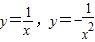 组合1种,lnx,
组合1种,lnx,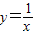 组合1种,共计4种都满足得一等奖的要求.
组合1种,共计4种都满足得一等奖的要求.
设“学生丙抽一次获得一等奖”为事件C,∴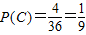 .
.
答:甲乙丙三人各得三、二、一等奖的概率分别是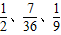 .…12分.
.…12分.
点评:本题考查古典概型及其概率计算公式的应用,体现了分类讨论的数学思想,属于基础题.
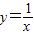 ,
,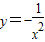 这三个函数可作为其它函数的导数,由此求得学生甲抽一次获得三等奖的概率.
这三个函数可作为其它函数的导数,由此求得学生甲抽一次获得三等奖的概率.(Ⅱ)在六个函数的卡片中,先后抽两次,不同的抽法有36种.其中,有7种抽法满足得二等奖的要求,由此求得学生乙抽一次获得二等奖的概率.
(Ⅲ)在六个函数的卡片中,先后抽两次,不同的抽法有36种.其中,有4种抽法满足得一等奖的要求,由此求得学生丙抽一次获得一等奖的概率.
解答:解:(Ⅰ)在y=sinx,y=cosx,y=ex,
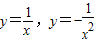 ,lnx六个函数中,y=cosx,
,lnx六个函数中,y=cosx,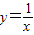 ,
,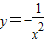 这三个函数可作为其它函数的导数.
这三个函数可作为其它函数的导数.设“学生甲抽一次获得三等奖”为事件A,∴
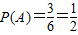 .…4分
.…4分(Ⅱ)在y=sinx,y=cosx,y=ex,
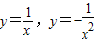 ,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种,
,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种,其中,y=sinx,y=cosx组合两种,y=ex,y=ex组合一种,
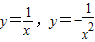 组合两种,lnx,
组合两种,lnx,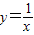 组合两种,共计7种都满足得二等奖的要求.
组合两种,共计7种都满足得二等奖的要求.设“学生乙抽一次获得二等奖”为事件B,∴
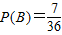 .…8分
.…8分(Ⅲ)在y=sinx,y=cosx,y=ex,
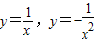 ,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种.
,lnx六个函数的卡片中,先后抽两次,不同的抽法有36种.其中,y=sinx,y=cosx组合1种,y=ex,y=ex组合1种,
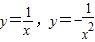 组合1种,lnx,
组合1种,lnx,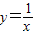 组合1种,共计4种都满足得一等奖的要求.
组合1种,共计4种都满足得一等奖的要求.设“学生丙抽一次获得一等奖”为事件C,∴
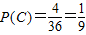 .
.答:甲乙丙三人各得三、二、一等奖的概率分别是
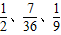 .…12分.
.…12分.点评:本题考查古典概型及其概率计算公式的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
|
班级 |
一班 |
二班 |
三班 |
四班 |
|
人数 |
2人 |
3人 |
4人 |
1人 |
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为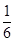 ;选择
;选择 音乐的概率都为
音乐的概率都为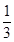 ;选择
;选择 读书的概率都为
读书的概率都为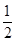 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量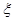 ,求随机变量
,求随机变量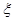 的分布列及数学期望
的分布列及数学期望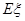 .
.
为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
|
班级 |
一班 |
二班 |
三班 |
四班 |
|
人数 |
2人 |
3人 |
4人 |
1人 |
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为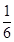 ;选择
;选择 音乐的概率都为
音乐的概率都为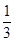 ;选择
;选择 读书的概率都为
读书的概率都为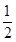 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量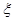 ,求随机变量
,求随机变量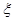 的分布列及数学期望
的分布列及数学期望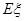 .
.