题目内容
（本题满分12分）下面的茎叶图是某班在一次测验时的成绩，程序用同时统计女生、男生及全班成绩的平均分，试回答下列问题：
（1） 在程序中，“=0”的含义是什么？
横线①处应填什么？
（2） 执行程序，输出S，T，A的值分别是多少？
（3） 请分析该班男女生的习情况．
(1)=0表示女生，横线①处应填：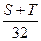
4分
（2）S="78 " T=76.9(或76.88或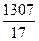
或77) A
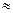77.4 8分
(3) 女生成绩比较集中，整体水平稍高于男生；男生中的高分段比女生高，低分段比女生多，相比较男生两极分化比较严重． 12分
解析
综合自测系列答案（本题满分12分）
调查某初中1000名学生的肥胖情况，得下表：
|
|
偏瘦 |
正常 |
肥胖 |
|
女生（人） |
100 |
173 |
|
|
男生（人） |
|
177 |
|
已知从这批学生中随机抽取1名学生，抽到偏瘦男生的概率为0.15。
（1）求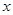
的值；
（2）若用分层抽样的方法，从这批学生中随机抽取50名，问应在肥胖学生中抽多少名？
（3）已知
，
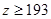，肥胖学生中男生不少于女生的概率。
（3）在（2）的条件下，若AB=2，AC=
，求三棱锥P-ABC的体积
（本题满分12分）下表是某班英语和数学成绩的分布表，已知该班有50名学生，成绩分为1~5个档次。如：表中英语成绩是4分、数学成绩是2分的人数有5人。现设该班任意一位学生的英语成绩为m,数学成绩为n。
|
n m |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英 语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
b |
6 |
0 |
a |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
（1）求m=4,n=3的概率；
（2）求在m≥3的条件下，n=3的概率；
（3）求a+b的值，并求m的数学期望；
（4）若m=2与n=4是相互独立的，求a，b的值。
（本题满分12分）下表是某小卖部6天卖出热茶的杯数与当天气温的对比表：
|
气温/℃ |
26 |
18 |
13 |
10 |
4 |
－1 |
|
杯数 |
20 |
24 |
34 |
38 |
50 |
64 |
（Ⅰ）将上表中的数据制成散点图,并判断散点图中温度与饮料杯数是否成线性相关关系?
（Ⅱ）如果把上述关系近似成线性关系的话，经计算得回归方程
= bx+ a的系数 b= -1.65，请求出回归直线方程来近似地表示这种线性关系.（a的值精确到0.1）
（Ⅲ）如果某天的气温是－5℃时，预测这天小卖部卖出热茶的杯数.
（本题满分12分）下表是某小卖部6天卖出热茶的杯数与当天气温的对比表：
| 气温/℃ | 26 | 18 | 13 | 10 | 4 | －1 |
| 杯数 | 20 | 24 | 34 | 38 | 50 | 64 |
（Ⅰ）将上表中的数据制成散点图,并判断散点图中温度与饮料杯数是否成线性相关关系?
（Ⅱ）如果把上述关系近似成线性关系的话，经计算得回归方程
= bx+ a的系数 b= -1.65，请求出回归直线方程来近似地表示这种线性关系.（a的值精确到0.1）
（Ⅲ）如果某天的气温是－5℃时，预测这天小卖部卖出热茶的杯数.