题目内容
已知函数f(x)=2cos2x―sin(2x― ).
).
(Ⅰ)求函数 的最大值,并写出
的最大值,并写出 取最大值时x的取值集合;
取最大值时x的取值集合;
(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(A)= ,b+c=2,求实数a的最小值。
,b+c=2,求实数a的最小值。
 ).
).(Ⅰ)求函数
 的最大值,并写出
的最大值,并写出 取最大值时x的取值集合;
取最大值时x的取值集合;(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=
 ,b+c=2,求实数a的最小值。
,b+c=2,求实数a的最小值。(Ⅰ)所以函数 的最大值为2,
的最大值为2, 取最大值时
取最大值时 的取值集合
的取值集合 ;(Ⅱ)实数
;(Ⅱ)实数 的最小值为1.
的最小值为1.
 的最大值为2,
的最大值为2, 取最大值时
取最大值时 的取值集合
的取值集合 ;(Ⅱ)实数
;(Ⅱ)实数 的最小值为1.
的最小值为1.试题分析:(Ⅰ)求函数
 的最大值,并写出
的最大值,并写出 取最大值时
取最大值时 的取值集合,首先将
的取值集合,首先将 化为一个角的一个三角函数,因此利用二倍角公式及辅助角公式,化简函数得
化为一个角的一个三角函数,因此利用二倍角公式及辅助角公式,化简函数得 ,即可求得函数的最大值为2,从而可得
,即可求得函数的最大值为2,从而可得 取最大值时
取最大值时 的取值集合;(Ⅱ)由(Ⅰ)得,
的取值集合;(Ⅱ)由(Ⅰ)得, ,故
,故 ,可求得角
,可求得角 的值为
的值为 ,在
,在 中,因为
中,因为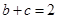 ,可考虑利用余弦定理来解,由余弦定理得,
,可考虑利用余弦定理来解,由余弦定理得, ,即可求得实数
,即可求得实数 的最小值.
的最小值.试题解析:(Ⅰ)f(x)=2cos2x-sin(2x-
 )=(1+cos2x)-(sin2xcos
)=(1+cos2x)-(sin2xcos -cos2xsin
-cos2xsin )
)=1+
 sin2x+
sin2x+ cos2x=sin(2x+
cos2x=sin(2x+ )+1 (3分)
)+1 (3分)所以函数
 的最大值为2. (4分)
的最大值为2. (4分)此时sin(2x+
 )=1,即2x+
)=1,即2x+ =2kπ+
=2kπ+ (k
(k z) 解得x=kπ+
z) 解得x=kπ+ (k
(k z)
z)故x的取值集合为
 {x| x=kπ+
{x| x=kπ+ ,k
,k z} (6分)
z} (6分)(Ⅱ)由题意f(A)=sin(2A+
 )+1=
)+1= ,化简得sin(2A+
,化简得sin(2A+ )=
)= ,
,∵A
 (0,π),
(0,π),  2A+
2A+
 (
( ,
, ).
).  A=
A= (8分)
(8分) 在三角形ABC中,根据余弦定理,
得a2=b2+c2-2bc·cos
 =(b+c)2-3bc (10分)
=(b+c)2-3bc (10分)由b+c="2" 知bc
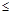 (
( )2="1," 即a2
)2="1," 即a2 1
1  当b=c=1时,实数a的最小值为1. (12分)
当b=c=1时,实数a的最小值为1. (12分)
练习册系列答案
相关题目
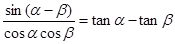
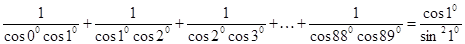
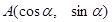 .
.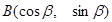 ,其中
,其中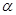 、
、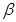 为锐角,且
为锐角,且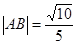 .
.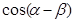 的值;
的值;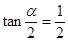 ,求
,求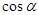 及
及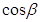 的值.
的值. .
. 的最大值及取得最大值时x的值;
的最大值及取得最大值时x的值; ,
, ,
, ,求△ABC的面积.
,求△ABC的面积.

 ,
,
 时,求函数
时,求函数 的值域;
的值域;
 ,当
,当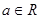 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. .
. 在区间
在区间 上的零点;
上的零点; ,求函数
,求函数 的图象的对称轴方程
的图象的对称轴方程 +sinα=-
+sinα=- ,-
,- <α<0,则cosα=__________.
<α<0,则cosα=__________. 中,若
中,若 ,则
,则 且
且 ,则
,则 =( )
=( )