题目内容
以椭圆 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线 的渐近线相切的圆的方程是 ( )
的渐近线相切的圆的方程是 ( )
A.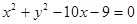 B.
B.
C. D.
D.
【答案】
B
【解析】略

练习册系列答案
相关题目
题目内容
以椭圆 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线 的渐近线相切的圆的方程是 ( )
的渐近线相切的圆的方程是 ( )
A.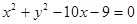 B.
B.
C. D.
D.
B
【解析】略
