题目内容
已知3,5,21是各项均为整数的无穷等差数列{an}的三项,若数列{an}的首项为a1,公差为d,给出关于数列{an}的4个命题:1满足条件的d有8个不同的取值;2存在满足条件的数列{an},使得对任意的n∈N*,都有S2n=4Sn成立;3对任意满足条件的d,存在a1,使得99一定是数列{an}中的一项;4对任意满足条件的d,存在a1,使得30一定是数列{an}中的一项;则其中所有正确命题的序号是 .
【答案】分析:由题意得,公差d可能为1,2,-1,-2,共4个不同的值,故1不正确.根据4个不同公差,分别求出S2n和Sn的值,经检验2不正确.根据4个不同公差,分别求出首项a1,经检验3、4正确.
解答:解:∵3,5,21是各项均为整数的无穷等差数列{an}的三项,∴公差d 可能为1,2,-1,-2,共4个不同的值.
故1不正确.
当d=1时,sn=na1+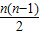 ,s2n=2na1+
,s2n=2na1+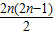 ,S2n=4Sn 不成立,
,S2n=4Sn 不成立,
同理,当d=-1时,S2n=4Sn不成立.
当d=2时,sn=na1+n(n-1),,s2n=2na1+2n(2n-1),S2n=4Sn 不成立,
同理,当 当d=-2时,S2n=4Sn 不成立,故 2不正确.
当d=1时,通项公式为 an=a1+(n-1),令99=a1+(n-1),a1=100-n.
同理当d=-1时,通项公式为 an=a1-(n-1),令99=a1-(n-1),a1=98+n.
当d=2时,通项公式为 为 an=a1+2(n-1),令99=a1+2(n-1),a1=101-2n..
当d=-2时,通项公式为 为 an=a1-2(n-1),令99=a1-2(n-1),a1=97+2n..故3正确.
当d=1时,通项公式为 an=a1+(n-1),令30=a1+(n-1),a1=31-n.
同理当d=-1时,通项公式为 an=a1-(n-1),令30=a1-(n-1),a1=29+n.
当d=2时,通项公式为 为 an=a1+2(n-1),令30=a1+2(n-1),a1=32-2n..
当d=-2时,通项公式为 为 an=a1-2(n-1),令30=a1-2(n-1),a1=28+2n..故4正确..
故答案为 3 4
点评:本题考查等差数列的通项公式及前n项和公式的应用,体现了分类讨论的数学思想,求出首项时间诶体的关键.
解答:解:∵3,5,21是各项均为整数的无穷等差数列{an}的三项,∴公差d 可能为1,2,-1,-2,共4个不同的值.
故1不正确.
当d=1时,sn=na1+
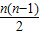 ,s2n=2na1+
,s2n=2na1+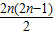 ,S2n=4Sn 不成立,
,S2n=4Sn 不成立,同理,当d=-1时,S2n=4Sn不成立.
当d=2时,sn=na1+n(n-1),,s2n=2na1+2n(2n-1),S2n=4Sn 不成立,
同理,当 当d=-2时,S2n=4Sn 不成立,故 2不正确.
当d=1时,通项公式为 an=a1+(n-1),令99=a1+(n-1),a1=100-n.
同理当d=-1时,通项公式为 an=a1-(n-1),令99=a1-(n-1),a1=98+n.
当d=2时,通项公式为 为 an=a1+2(n-1),令99=a1+2(n-1),a1=101-2n..
当d=-2时,通项公式为 为 an=a1-2(n-1),令99=a1-2(n-1),a1=97+2n..故3正确.
当d=1时,通项公式为 an=a1+(n-1),令30=a1+(n-1),a1=31-n.
同理当d=-1时,通项公式为 an=a1-(n-1),令30=a1-(n-1),a1=29+n.
当d=2时,通项公式为 为 an=a1+2(n-1),令30=a1+2(n-1),a1=32-2n..
当d=-2时,通项公式为 为 an=a1-2(n-1),令30=a1-2(n-1),a1=28+2n..故4正确..
故答案为 3 4
点评:本题考查等差数列的通项公式及前n项和公式的应用,体现了分类讨论的数学思想,求出首项时间诶体的关键.

练习册系列答案
相关题目
由于卫生的要求游泳池要经常换水(进一些干净的水同时放掉一些脏水),游泳池的水深经常变化,已知泰州某浴场的水深y(米)是时间t(0≤t≤24),(单位小时)的函数,记作y=f(t),下表是某日各时的水深数据经长期观测的曲线y=f(t)可近似地看成函数y=Acosωt+b
(Ⅰ)根据以上数据,求出函数y=Acosωt+b的最小正周期T,振幅A及函数表达式;
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多少时间可供游泳爱好者进行运动.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 2 5 | 2 0 | 15 | 20 | 249 | 2 | 151 | 199 | 2 5 |
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,判断一天内的上午8:00至晚上20:00之间,有多少时间可供游泳爱好者进行运动.
已知某海滨浴场的海浪高度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t),下表是某日各时的浪高数据:
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b.
(1)求函数y=Acosωt+b的最小正周期T,振幅A及函数表达式.
(2)依据规定:当海浪高度高于1m时才对冲浪爱好者开放,请依据(1)的结论,一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动.
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)求函数y=Acosωt+b的最小正周期T,振幅A及函数表达式.
(2)依据规定:当海浪高度高于1m时才对冲浪爱好者开放,请依据(1)的结论,一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动.
已知某海滨浴场的海浪高度y(单位:米)与时间 t(0≤t≤24)(单位:时)的函数关系记作y=f(t),下表是某日各时的浪高数据:
经长期观测,函数y=f(t)可近似地看成是函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T及函数表达 式(其中A>0,ω>0);
(2)根据规定,当海浪高度不低于0.75米时,才对冲浪爱好者开放,请根据以上结论,判断一天内从上午7时至晚上19时之间,该浴场有多少时间可向冲浪爱好者开放?
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T及函数表达 式(其中A>0,ω>0);
(2)根据规定,当海浪高度不低于0.75米时,才对冲浪爱好者开放,请根据以上结论,判断一天内从上午7时至晚上19时之间,该浴场有多少时间可向冲浪爱好者开放?