题目内容
设a>0,解关于x的不等式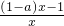 <0.
<0.
解:不等式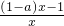 <0可化为x•[(1-a)x-1]<0
<0可化为x•[(1-a)x-1]<0
①当0<a<1时,有 >0,
>0,
此时不等式的解析为(0, )
)
②当a=1时,此时不等式的解析为(0,+∞)
③当a>1时,有 <0,
<0,
此时不等式的解析为(-∞, )∪(0,+∞)
)∪(0,+∞)
分析:不等式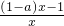 <0可化为x•[(1-a)x-1]<0,我们分0<a<1时,a=1时,a>1时,三种情况讨论不等式的解集,最后综合讨论结果,即可得到答案.
<0可化为x•[(1-a)x-1]<0,我们分0<a<1时,a=1时,a>1时,三种情况讨论不等式的解集,最后综合讨论结果,即可得到答案.
点评:本题考查的知识点是一元二次不等式的解法,其中当不等式中遇到参数无法确定时,常引入分类讨论的方法.
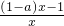 <0可化为x•[(1-a)x-1]<0
<0可化为x•[(1-a)x-1]<0①当0<a<1时,有
 >0,
>0,此时不等式的解析为(0,
 )
)②当a=1时,此时不等式的解析为(0,+∞)
③当a>1时,有
 <0,
<0,此时不等式的解析为(-∞,
 )∪(0,+∞)
)∪(0,+∞)分析:不等式
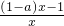 <0可化为x•[(1-a)x-1]<0,我们分0<a<1时,a=1时,a>1时,三种情况讨论不等式的解集,最后综合讨论结果,即可得到答案.
<0可化为x•[(1-a)x-1]<0,我们分0<a<1时,a=1时,a>1时,三种情况讨论不等式的解集,最后综合讨论结果,即可得到答案.点评:本题考查的知识点是一元二次不等式的解法,其中当不等式中遇到参数无法确定时,常引入分类讨论的方法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 <0.
<0.