题目内容
已知函数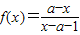 的反函数f-1(x)的图象对称中心是(-1,
的反函数f-1(x)的图象对称中心是(-1, ),则函数h(x)=loga(x2-2x)的单调递增区间是( )
),则函数h(x)=loga(x2-2x)的单调递增区间是( )A.(1,+∞)
B.(-∞,1)
C.(-∞,0)
D.(2,+∞)
【答案】分析:根据反函数f-1(x)的图象对称中心求出f(x)的对称中心,根据复合函数的单调性遵循:同增异减,求出复合函数h(x)=loga(x2-2x)的单调递增区间.
解答:解:因为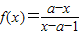 的反函数f-1(x)的图象对称中心是(-1,
的反函数f-1(x)的图象对称中心是(-1, ),
),
所以f(x)关于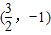 对称,
对称,
因为f(x)=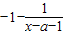
所以a+1=
所以a=
所以h(x)=loga(x2-2x)=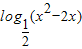
h(x)的定义域为{x|x>2或x<0}
令t=x2-2x=(x-1)2-1在(2,+∞)递增;在(-∞,0)递减;
因为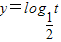 为减函数,
为减函数,
所以函数h(x)=loga(x2-2x)的单调递增区间是(-∞,0)
故选C.
点评:本题考查复合函数的单调性:遵循同增异减;考查互为反函数关于y=x对称,其对称中心也关于y=x对称.
解答:解:因为
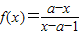 的反函数f-1(x)的图象对称中心是(-1,
的反函数f-1(x)的图象对称中心是(-1, ),
),所以f(x)关于
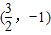 对称,
对称,因为f(x)=
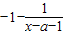
所以a+1=

所以a=

所以h(x)=loga(x2-2x)=
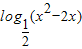
h(x)的定义域为{x|x>2或x<0}
令t=x2-2x=(x-1)2-1在(2,+∞)递增;在(-∞,0)递减;
因为
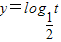 为减函数,
为减函数,所以函数h(x)=loga(x2-2x)的单调递增区间是(-∞,0)
故选C.
点评:本题考查复合函数的单调性:遵循同增异减;考查互为反函数关于y=x对称,其对称中心也关于y=x对称.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
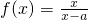 的反函数f-1(x)的图象的对称中心是(1,2),则a=________.
的反函数f-1(x)的图象的对称中心是(1,2),则a=________.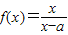 的反函数f-1(x)的图象的对称中心是(1,2),则a= .
的反函数f-1(x)的图象的对称中心是(1,2),则a= .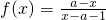 的反函数f-1(x)的图象对称中心是(-1,
的反函数f-1(x)的图象对称中心是(-1, ),则函数h(x)=loga(x2-2x)的单调递增区间是
),则函数h(x)=loga(x2-2x)的单调递增区间是