题目内容
 如图,平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为| π |
| 4 |
分析:连接AB′,BA′,由题设知∠B′AB=
,AA′⊥β,BB′⊥α,∠ABA′是AB与平面β所成的角,由此能求出AB与平面β所成的角的正弦值.
| π |
| 4 |
解答: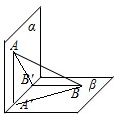 解:连接AB‘,BA’,
解:连接AB‘,BA’,
∵平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
,
过A、B分别作两平面交线的垂线,垂足为A′、B′,
∴∠B′AB=
,AA′⊥β,BB′⊥α,∠ABA′是AB与平面β所成的角,
设A′B′=a,∵AB=3A'B',∴AB=3a,
设AB′=BB′=x,则2x2=9a2,解得AB′=BB′=
a,
∴A′B=
=
a ,AA′=
=
a,
∴sin∠ABA′=
=
.
故选A.
 解:连接AB‘,BA’,
解:连接AB‘,BA’,∵平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
| π |
| 4 |
过A、B分别作两平面交线的垂线,垂足为A′、B′,
∴∠B′AB=
| π |
| 4 |
设A′B′=a,∵AB=3A'B',∴AB=3a,
设AB′=BB′=x,则2x2=9a2,解得AB′=BB′=
3
| ||
| 2 |
∴A′B=
|
| ||
| 2 |
9a2-
|
| ||
| 2 |
∴sin∠ABA′=
| ||||
| 3a |
| ||
| 6 |
故选A.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.
如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.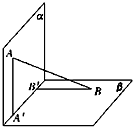 如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α、β所成的角分别为
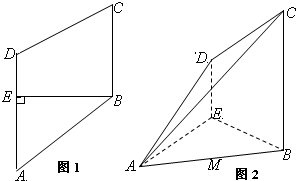 (2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC.设M是AB上的动点.
(2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC.设M是AB上的动点. 如图,平面
如图,平面