题目内容
已知f(x)=
，若|f（x）|≥ax在x∈[-1，1]上恒成立，则实数a的取值范围（ ）
|
| A、（-∞-1]∪[0，+∞） |
| B、[-1，0] |
| C、[0，1] |
| D、[-1，0） |
分析：先画出函数f(x)=
和|f（x）|的图象；利用图象再结合答案即可解决本题．
|
解答：解：函数f(x)=
的图象如图：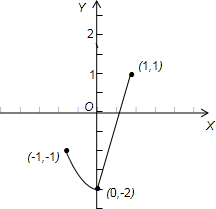
|f（x）|的图象如图：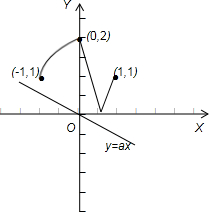
因为|f（x）|≥ax在x∈[-1，1]上恒成立，
所以y=ax的图象应在y=|f（x）|的图象的下方，
故须斜率为负，或为0．
当斜率为负时，排除答案A，C；
当a=0，y=0满足要求，排除D．
故选 B．
|
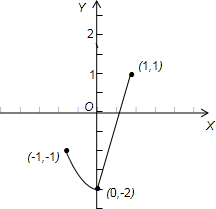
|f（x）|的图象如图：
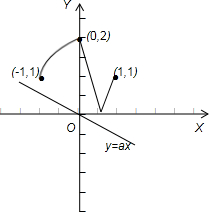
因为|f（x）|≥ax在x∈[-1，1]上恒成立，
所以y=ax的图象应在y=|f（x）|的图象的下方，
故须斜率为负，或为0．
当斜率为负时，排除答案A，C；
当a=0，y=0满足要求，排除D．
故选 B．
点评：本题主要考查函数的图象．其中涉及到二次函数，一次函数，分段函数以及带绝对值的函数的图象，是对函数的大汇总，在画整体带绝对值的函数图象时，注意起翻折原则是X轴上方的保持不变，X轴下方的沿x轴对折．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目