题目内容
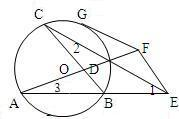已知圆O的两弦AB和CD延长相交于E，过E点引EF∥CB交AD的延长线于F，过F点作圆O的切线FG，求证：EF=FG．
分析：根据切割线定理得FG2=FD•FA，再利用两个三角形△EFD和△AFE相似，从而可求证得两线段相等．
解答：证明：∵FG为⊙O的切线，而FDA为⊙O的割线，
∴FG2=FD•FA①
又∵EF∥CB，
∴∠1=∠2．而∠2=∠3，
∴∠1=∠3，
∠EFD=∠AFE为公共角
∴△EFD∽△AFE，
=
，
即EF2=FD•FA②
由①，②可得EF2=FG2
∴EF=FG．
∴FG2=FD•FA①
又∵EF∥CB，
∴∠1=∠2．而∠2=∠3，
∴∠1=∠3，
∠EFD=∠AFE为公共角
∴△EFD∽△AFE，
| FD |
| EF |
| EF |
| FA |
即EF2=FD•FA②
由①，②可得EF2=FG2
∴EF=FG．
点评：本题主要是运用了切割线定理定理以及相似三角形知识，属于基础题，如何证三角形相似是解题的关键．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
附加题：（选做题：在下面A、B、C、D四个小题中只能选做两题）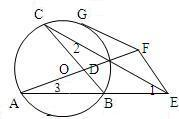
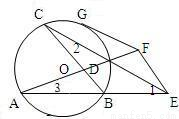已知圆O的两弦AB和CD延长相交于E，过E点引EF∥CB交AD的延长线于F，过F点作圆O的切线FG，求证：EF=FG．