题目内容
【题目】已知点A(﹣1,0),B(1,0),直线AM与直线BM相交于点M,直线AM与直线BM的斜率分别记为kAM与kBM , 且kAMkBM=﹣2 (Ⅰ)求点M的轨迹C的方程;
(Ⅱ)过定点F(0,1)作直线PQ与曲线C交于P,Q两点,△OPQ的面积是否存在最大值?若存在,求出△OPQ面积的最大值;若不存在,请说明理由.
【答案】解:(Ⅰ)由题意可得:设M(x,y), 所以直线AM与直线BM的斜率分别为 ![]() ,
, ![]() ,
,
因为直线AM与直线BM的斜率之积为﹣2,
所以 ![]()
![]() =﹣2,化简得:
=﹣2,化简得: ![]() =1(y≠0).
=1(y≠0).
所以动点M的轨迹C的方程为: ![]() =1(y≠0).
=1(y≠0).
(Ⅱ)由已知当直线PQ的斜率存在,设直线PQ的方程是y=kx+1,
联立直线与椭圆方程,消去y得(k2+2)x2+2kx﹣1=0,
∵△=(4k2)+4(k2+2)=8(k2+1)>0,∴k∈R,
设P(x1 , y1),Q(x2 , y2),x1+x2=﹣ ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
S△OPQ= ![]() |x1﹣x2|=
|x1﹣x2|= ![]() =
= 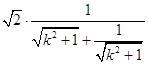 ≤
≤ ![]()
当且仅当k=0时取等号,
△OPQ面积的最大值为 ![]()
【解析】(Ⅰ)设M(x,y),由kMA×kMB=﹣2,得 ![]()
![]() =﹣2,由此能求出点M的轨迹C的方程.(Ⅱ)由已知当直线PQ的斜率存在,设直线PQ的方程是y=kx+1,与椭圆联立,得(k2+2)x2+2kx﹣1=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出△OPQ面积的最大值.
=﹣2,由此能求出点M的轨迹C的方程.(Ⅱ)由已知当直线PQ的斜率存在,设直线PQ的方程是y=kx+1,与椭圆联立,得(k2+2)x2+2kx﹣1=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出△OPQ面积的最大值.

练习册系列答案
相关题目