题目内容
已知 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数 在
在 上只有一个零点,求实数
上只有一个零点,求实数 的取值范围.
的取值范围.
(Ⅰ) 和
和 ;(Ⅱ)
;(Ⅱ) 或
或
解析试题分析:1.本题要注意函数的定义域 .2.在比较
.2.在比较 与
与 的大小时,如果直接采用作差的方式进行比较:
的大小时,如果直接采用作差的方式进行比较:
 ,则很难得出答案.实际上,因为
,则很难得出答案.实际上,因为 ,
, ,所以
,所以 .这提示我们处理问题的时候思维要相当灵活,要眼观六路,耳听八方,怎么好做就怎么做.
.这提示我们处理问题的时候思维要相当灵活,要眼观六路,耳听八方,怎么好做就怎么做.
3. 很多考生误认为 在
在 上只有一个零点
上只有一个零点 事实上漏了
事实上漏了 .
.
试题解析:(Ⅰ) 的定义域为
的定义域为 .
.
∵
∴ .
.
解 得
得 或
或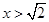 .
.
∴ 的单调递增区间是
的单调递增区间是 和
和 .
.
(Ⅱ)由已知得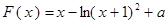 ,且
,且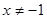 .
.
∴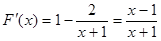 .
.
∴当 或
或 时,
时, ;
;
当 时,
时, .
.
∴当 时,
时, ,此时,
,此时,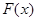 单调递减;
单调递减;
当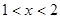 时,
时, ,此时,
,此时,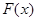 单调递增.
单调递增.
∵ ,
, ,
,
∴ .
.
∴ 在
在 上只有一个零点
上只有一个零点 或
或 .
.
由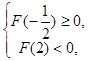 得
得 ;
;
由 ,得
,得 .
.
∴实数 的取值范围为
的取值范围为 或
或
考点:函数的单调性、极值、零点、比较大小.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,
,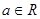
 时,求曲线
时,求曲线 在点
在点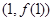 处的切线方程;
处的切线方程;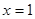 处有极值,求
处有极值,求 ,使
,使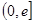 的最小值是3,若存在,求出
的最小值是3,若存在,求出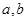 是实数,函数
是实数,函数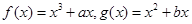 ,
,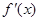 和
和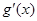 ,分别是
,分别是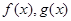 的导函数,若
的导函数,若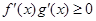 在区间
在区间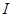 上恒成立,则称
上恒成立,则称 和
和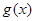 在区间
在区间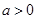 ,若函数
,若函数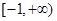 上单调性一致,求实数
上单调性一致,求实数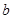 的取值范围;
的取值范围;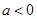 且
且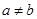 ,若函数
,若函数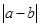 的最大值.
的最大值.
 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 (
( )成立,求实数
)成立,求实数 .
.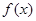 的单调区间;
的单调区间;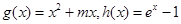 ,若在
,若在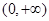 上至少存在一点
上至少存在一点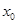 ,使得
,使得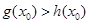 成立,求
成立,求 的范围.
的范围. ,
, 为自然对数的底数).
为自然对数的底数).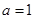 时,求
时,求 的单调区间;
的单调区间; 上无零点,求
上无零点,求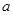 最小值;
最小值; ,在
,在 上总存在两个不同的
上总存在两个不同的
 ),使
),使 成立,求
成立,求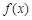 是定义在
是定义在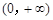 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记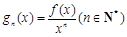 .若对定义域内的每一个
.若对定义域内的每一个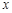 ,总有
,总有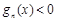 ,则称
,则称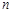 阶负函数”;若对定义域内的每一个
阶负函数”;若对定义域内的每一个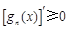 ,
,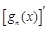 为函数
为函数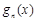 的导函数).
的导函数). 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数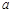 的取值范围;
的取值范围;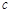 ,使得
,使得 恒成立,试判断
恒成立,试判断 在
在 与
与 处都取得极值.
处都取得极值.  ,
, 的值;
的值; ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得、
,使得、 ,求实数
,求实数 的取值范围.
的取值范围. 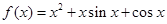 .
.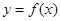 在点
在点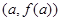 处与直线
处与直线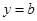 相切,求
相切,求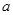 与
与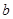 的值.
的值.