题目内容
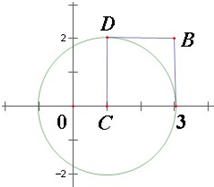 已知圆C:(x-1)2+y2=4,点(a,b).
已知圆C:(x-1)2+y2=4,点(a,b).(1)若a是从1,2,3三个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求点(a,b)在圆C内的概率;
(2)若a是从区间[1,3]任取的一个数,b是从区间[0,2]任取的一个数,求点(a,b)在圆C外的概率.
分析:(1)求得所有的(a,b)共9个,而满足条件的(a,b)共4个,由此求得所求事件的概率.
(2)试验的所有基本事件所构成的区域为边长是2的正方形,其中所求事件的区域为图中阴影部分,由几何概型的计算公式即可得到所求事件发生的概率.
(2)试验的所有基本事件所构成的区域为边长是2的正方形,其中所求事件的区域为图中阴影部分,由几何概型的计算公式即可得到所求事件发生的概率.
解答: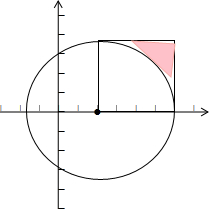 解:(1)用数对(a,b)表示基本事件,则其所有可能结果有:
解:(1)用数对(a,b)表示基本事件,则其所有可能结果有:
(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个.
事件A={点(a,b)在圆C内},其结果为:(1,0),(1,1),(2,0),(2,1)共4个
所以P(A)=
(2)所有可能结果Ω={(a,b)|
}表示的区域图中正方形ABDC,
事件B={点(a,b)在圆C外}表示的区域为图中阴影部分
所以P(B)=
=1-
.
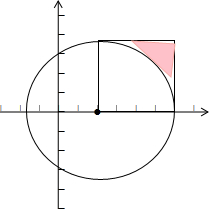 解:(1)用数对(a,b)表示基本事件,则其所有可能结果有:
解:(1)用数对(a,b)表示基本事件,则其所有可能结果有:(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个.
事件A={点(a,b)在圆C内},其结果为:(1,0),(1,1),(2,0),(2,1)共4个
所以P(A)=
| 4 |
| 9 |
(2)所有可能结果Ω={(a,b)|
|
事件B={点(a,b)在圆C外}表示的区域为图中阴影部分
所以P(B)=
2×2-
| ||
| 2×2 |
| π |
| 4 |
点评:本题考查了古典概型及其概率计算公式,考查了几何概型的概率,关键是理解(2)的测度比,是基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目