题目内容
已知 在区间
在区间 上是增函数,实数
上是增函数,实数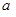 组成集合
组成集合 ;设关于
;设关于 的方程
的方程 的两个非零实根
的两个非零实根 实数
实数 使得不等式
使得不等式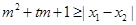 使得对任意
使得对任意 及
及 恒成立,则
恒成立,则 的解集是( )
的解集是( )
A. | B. |
C. | D. |
A
解析试题分析:∵f(x)在[-1,1]上是增函数,
∴f'(x)≥0对x∈[-1,1]恒成立,
即x2-ax-2≤0对x∈[-1,1]恒成立.①
设φ(x)=x2-ax-2,
方法一:①?φ(1)=1-a-2≤0且φ(-1)=1+a-2≤0?-1≤a≤1,
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
方法二:
①? ,φ(-1)=1+a-2≤0或
,φ(-1)=1+a-2≤0或 ,φ(1)=1-a-2≤0?0≤a≤1或-1≤a≤0
,φ(1)=1-a-2≤0?0≤a≤1或-1≤a≤0
?-1≤a≤1.
∵对x∈[-1,1],f(x)是连续函数,且只有当a=1时,f'(-1)=0以及当a=-1时,f'(1)=0
∴A={a|-1≤a≤1}.
由 =
= ,得x2-ax-2=0,∵△=a2+8>0,∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,从而|x1-x2|==
,得x2-ax-2=0,∵△=a2+8>0,∴x1,x2是方程x2-ax-2=0的两非零实根,x1+x2=a,x1x2=-2,从而|x1-x2|== =
= ∵-1≤a≤1,∴|x1-x2|=
∵-1≤a≤1,∴|x1-x2|= ≤3.
≤3.
要使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,
当且仅当m2+tm+1≥3对任意t∈[-1,1]恒成立,
即m2+tm-2≥0对任意t∈[-1,1]恒成立.②
设g(t)=m2+tm-2=mt+(m2-2),
方法一:
②?g(-1)=m2-m-2≥0,g(1)=m2+m-2≥0,
?m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.,
方法二:
当m=0时,②显然不成立;
当m≠0时,
②?m>0,g(-1)=m2-m-2≥0或m<0,g(1)=m2+m-2≥0
?m≥2或m≤-2.
所以,存在实数m,使不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立,其取值范围是{m|m≥2,或m≤-2}.,选A.
考点:本题主要考查函数的单调性,导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力。
点评:解决该试题的关键是根据一元二次方程根与系数的关系写出不等式先看成关于a的不等式恒成立再看成关于t的一次不等式恒成立,让两端点大等于零,以及函数单调递增导数大于等于零列出不等式解之

已知函数 (
( 为常数,且
为常数,且 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数 、
、 ,恒有
,恒有 成立,则正整数
成立,则正整数 可以取的值有
可以取的值有
| A.4个 | B.5个 | C.6 个 | D.7个 |
下列各组函数中,表示同一个函数的是
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
若 ,则
,则 的定义域为
的定义域为
A. | B. | C. | D. |
函数 的单调递减区间是 ( )
的单调递减区间是 ( )
A. | B. | C. | D. |
已知数列 满足:
满足: ,则
,则 =( )
=( )
A. | B. | C. | D. |
设函数 的图像的交点为
的图像的交点为 ,则x0所在的区间是
,则x0所在的区间是
A. | B. | C. | D. |
已知函数 的图象如图所示,则
的图象如图所示,则 满足的关系是( )
满足的关系是( )
A. | B.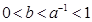 |
C. | D. |
 与
与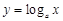 的图象可能是( )
的图象可能是( )