题目内容
经研究发现,学生的接受能力依赖于老师引入概念和描述总量所用的时间,开始讲题时,学生的兴趣保持较理想的状态,随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示提出和讲授概念的时间(单位:分),有以下的公式:f(x)=

(1)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强呢?
(2)开讲后多少分钟,学生的接受能力最强?能维持多长的时间?
(3)若讲解这道数学题需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲完这道题?
【答案】分析:(1)分别计算出f(5),f(20)再比较它们的大小f(5)、f(20)即可得出开讲后5分钟学生的接受能力比开讲后20分钟强.
(2)分两类讨论函数的最大值:①当0<x≤10时,②当16<x<30时,从而得出开讲后10钟学生达到最强的接受能力,并维持6分钟.
(3)分两种情形讨论:①当0<x<10时,②当16<x<30时,分别令f(x)>55,求得相应x的取值范围,得出结论:学生达到或超过55的接受能力的时间11.3分钟,小于13分钟,故这位老师不能在学生所需状态下讲完这道题.
解答:解:(1)f(5)=53.5,f(20)=47⇒f(5)>f(20)⇒.
开讲后5分钟学生的接受能力比开讲后20分钟强.
(2)当0<x≤10时,f(x)=-0.1(x-13)2+59.9⇒f(x)是增函数⇒最大值是
f(10)=59;当16<x<30时,f(x)是递减的函数,
⇒f(x)<f(16)=59,故开讲后10钟学生达到最强的接受能力,并维持6分钟.
(3)当0<x<10时,令f(x)>55,则6<x<10;
当16<x<30时,令f(x)>55,则16<x<17.3
因此,学生达到或超过55的接受能力的时间11.3分钟,
小于13分钟,故这位老师不能在学生所需状态下讲完这道题.
点评:本题函数模型为分段函数,分段函数模型的构造中,自变量取值的分界是关键点,只有合理的分类,正确的求解才能成功地解题.但分类时要做到不重不漏.正确求出函数解析式后,利用函数的常规方法求解相关问题.求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.
(2)分两类讨论函数的最大值:①当0<x≤10时,②当16<x<30时,从而得出开讲后10钟学生达到最强的接受能力,并维持6分钟.
(3)分两种情形讨论:①当0<x<10时,②当16<x<30时,分别令f(x)>55,求得相应x的取值范围,得出结论:学生达到或超过55的接受能力的时间11.3分钟,小于13分钟,故这位老师不能在学生所需状态下讲完这道题.
解答:解:(1)f(5)=53.5,f(20)=47⇒f(5)>f(20)⇒.
开讲后5分钟学生的接受能力比开讲后20分钟强.
(2)当0<x≤10时,f(x)=-0.1(x-13)2+59.9⇒f(x)是增函数⇒最大值是
f(10)=59;当16<x<30时,f(x)是递减的函数,
⇒f(x)<f(16)=59,故开讲后10钟学生达到最强的接受能力,并维持6分钟.
(3)当0<x<10时,令f(x)>55,则6<x<10;
当16<x<30时,令f(x)>55,则16<x<17.3
因此,学生达到或超过55的接受能力的时间11.3分钟,
小于13分钟,故这位老师不能在学生所需状态下讲完这道题.
点评:本题函数模型为分段函数,分段函数模型的构造中,自变量取值的分界是关键点,只有合理的分类,正确的求解才能成功地解题.但分类时要做到不重不漏.正确求出函数解析式后,利用函数的常规方法求解相关问题.求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
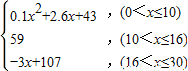
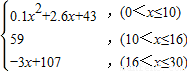
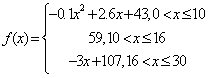 。
。