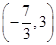题目内容
若关于x的不等式2-|x-a|>x2至少有一个负数解,则实数a的取值范围是( )
分析:解法1:通过给变量取特殊值,举反例可得选项B、C、D不正确,从而选出A.
解法2:在同一坐标系内作出函数y=-x2+2和y=|x-a|的图象,结合图象从而求得|x-a|<-x2+2的解集.
解法2:在同一坐标系内作出函数y=-x2+2和y=|x-a|的图象,结合图象从而求得|x-a|<-x2+2的解集.
解答:解:解法1:取a=-2,得不等式2-|x+2|>x2有负数解x=-
,排除选项B、C,取a=
,
不等式2-|x-
|>x2无负数解,排除D,故选A.
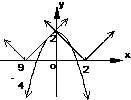
解法2:将原不等式变形为|x-a|<-x2+2,在同一坐标系内作出函数y=-x2+2
和y=|x-a|的图象,
函数y=|x-a|的图象是从点(a,0)出发的两条射线,如图,
当射线y=-x+a(x≤a)过点(0,2)时,a=2,
当射线y=x-a(x≥a)与抛物线y=-x2+2相切时,把y=x-a代入y=-x2+2 化简可得x2+x-a-2=0,
由判别式等于0可得△=1+4(a+2)=0,解得 a=-
,
结合图象易得-
<a<2.
| 1 |
| 2 |
| 5 |
| 2 |

不等式2-|x-
| 5 |
| 2 |
解法2:将原不等式变形为|x-a|<-x2+2,在同一坐标系内作出函数y=-x2+2
和y=|x-a|的图象,
函数y=|x-a|的图象是从点(a,0)出发的两条射线,如图,
当射线y=-x+a(x≤a)过点(0,2)时,a=2,
当射线y=x-a(x≥a)与抛物线y=-x2+2相切时,把y=x-a代入y=-x2+2 化简可得x2+x-a-2=0,
由判别式等于0可得△=1+4(a+2)=0,解得 a=-
| 9 |
| 4 |
结合图象易得-
| 9 |
| 4 |
点评:本题主要考查绝对值不等式的解法,体现了数形结合的数学思想,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
若关于x的不等式2-x2>|x-a|至少有一个负数解,则a的取值范围为( )
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(-
|
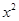 >|x-a|
至少有一个负数解,则实数a的取值范围是
.
>|x-a|
至少有一个负数解,则实数a的取值范围是
.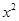 >|x-a| 至少有一个负数解,则a的取值范围为(
)
>|x-a| 至少有一个负数解,则a的取值范围为(
)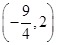 B.
B.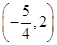 C.
C.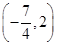 D.
D.