题目内容
设m,n∈N,f(x)=(1+x)m+(1+x)n,(1)当m=n=7时,若f(x)=a7x7+a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0求a0+a2+a4+a6.
(2)当m=n时,若f(x)展开式中x2的系数是20,求n的值.
(3)f(x)展开式中x的系数是19,当m,n变化时,求x2系数的最小值.
分析:(1)本题可以应用赋值法分别令x=1,x=-1,写出两个等式,把两个等式相加得到要求的下标是偶数的系数的和.
(2)写出二项式的展开式,根据当m=n时,f(x)展开式.中x2的系数是20,得到T3=2Cn2x2=20x2,求出n的值.
(3)要求一个系数的最小值,首先表示出这个项的系数,根据m,n之间的关系,代入系数的表示式,根据二次函数的最值求法得到结果.
(2)写出二项式的展开式,根据当m=n时,f(x)展开式.中x2的系数是20,得到T3=2Cn2x2=20x2,求出n的值.
(3)要求一个系数的最小值,首先表示出这个项的系数,根据m,n之间的关系,代入系数的表示式,根据二次函数的最值求法得到结果.
解答:解:(1)本题可以应用赋值法:分别令x=1,x=-1,
28=a7+a6+a5+a4+a3+a2+a1+a0
0=-a7+a6-a5+a4-a3+a2-a1+a0
两个式子相加得a0+a2+a4+a6=128…(4分)
(2)∵当m=n时,f(x)展开式中x2的系数是20,
∴T3=2Cn2x2=20x2,
∴n=5…(8分)
(3)当m+n=19,
x2的系数为:
+
=
m(m-1)+
n(n-1)
=
[(m+n)2-2mn-(m+n)]=171-mn=171-(19-n)n=(n-
)2+
∴当n=10或n=9时,f(x)展开式中x2的系数最小为81.…(12分)
28=a7+a6+a5+a4+a3+a2+a1+a0
0=-a7+a6-a5+a4-a3+a2-a1+a0
两个式子相加得a0+a2+a4+a6=128…(4分)
(2)∵当m=n时,f(x)展开式中x2的系数是20,
∴T3=2Cn2x2=20x2,
∴n=5…(8分)
(3)当m+n=19,
x2的系数为:
| C | 2 m |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 19 |
| 2 |
| 323 |
| 4 |
∴当n=10或n=9时,f(x)展开式中x2的系数最小为81.…(12分)
点评:本题考查二项式定理的应用,本题解题的关键是正确利用二项式的展开式,本题还结合二次函数的性质,是一个综合题目.

练习册系列答案
相关题目
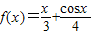 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; 是方程f(x)-x=0的实数根,求证:对于f(x)定义域中任意的x2,x3,当|x2-x1|<1,且|x3-x1|<1时,|f(x3)-f(x2)|<2.
是方程f(x)-x=0的实数根,求证:对于f(x)定义域中任意的x2,x3,当|x2-x1|<1,且|x3-x1|<1时,|f(x3)-f(x2)|<2.