题目内容
15．设p：函数f（x）=x2-2ax-1在区间（-∞，2]上单调递减，q：函数g（x）=lg（x2+ax+4）的定义域是R，如果命题“p或q”为真命题，“p且q”为假命题，求实数a的取值范围．分析 先求出关于p，q成立的a的范围，根据p，q一真一假，通过讨论得到关于a的不等式组，解出即可．
解答 解：关于p：函数f（x）=x2-2ax-1在区间（-∞，2]上单调递减，
∴对称轴x=a≥2；
关于q：函数g（x）=lg（x2+ax+4）的定义域是R，
∴x2+ax+4＞0恒成立，
∴△=a2-16＜0，解得：-4＜a＜4，
如果命题“p或q”为真命题，“p且q”为假命题，
则p，q一真一假，
p真q假时：$\left\{\begin{array}{l}{a≥2}\\{a≥4或a≤-4}\end{array}\right.$，解得：a≥4，
p假q真时：$\left\{\begin{array}{l}{a＜2}\\{-4＜a＜4}\end{array}\right.$，解得：-4＜a＜2，
综上a的范围是：（-4，2）∪[4，+∞）．
点评 本题考查了复合命题的判断，考查二次函数、对数函数的性质，是一道中档题．
练习册系列答案
相关题目
10．
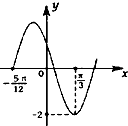已知函数f（x）=Acos（ωx+φ）（x∈R）的图象的一部分如图所示，其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$，为了得到函数f（x）的图象，只要将函数g（x）=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$（x∈R）图象上所有的点（ ）
已知函数f（x）=Acos（ωx+φ）（x∈R）的图象的一部分如图所示，其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$，为了得到函数f（x）的图象，只要将函数g（x）=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$（x∈R）图象上所有的点（ ）| A． | 向右平移$\frac{π}{6}$个单位长度，再把所得各点的横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变 | |
| B． | 向右平移$\frac{π}{6}$个单位长度，再把所得各点的横坐标变为原来的2倍；纵坐标不变 | |
| C． | 向左平移$\frac{π}{3}$个单位长度，再把得所各点的横坐标变为原来的$\frac{1}{2}$倍；纵坐标不变 | |
| D． | 向左平移$\frac{π}{3}$个单位长度，再把所得各点的横坐标变为原来的2倍，纵坐标不变 |
4．若△ABC为锐角三角形，则下列式子一定成立的是（ ）
| A． | logcosC$\frac{sinA}{cosB}$＞0 | B． | logsinC$\frac{cosA}{cosB}$＞0 | ||
| C． | logsinC$\frac{sinA}{sinB}$＞0 | D． | logsinC$\frac{cosA}{sinB}$＞0 |