题目内容
已知数列An:a1,a2,…,an,满足a1=an=0,且当2≤k≤n(k∈N*)时,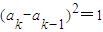 .令S(An)=a1+a2+…+an.
.令S(An)=a1+a2+…+an.(Ⅰ)写出S(A5)的所有可能取值;
(Ⅱ)求S(An)的最大值.
【答案】分析:(Ⅰ)根据新定义,分类,即可求S(A5)的所有可能取值;
(Ⅱ)由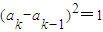 ,可设ak-ak-1=ck-1,可得an=a1+c1+c2+…+cn-1,根据a1=an=0,可得c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由
,可设ak-ak-1=ck-1,可得an=a1+c1+c2+…+cn-1,根据a1=an=0,可得c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由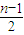 个1和
个1和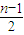 个-1构成的数列,由此可得当c1,c2,…,cn-1的前
个-1构成的数列,由此可得当c1,c2,…,cn-1的前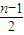 项取1,后
项取1,后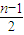 项取-1时S(An)最大.
项取-1时S(An)最大.
解答:解:(Ⅰ)由题设,满足条件的数列A5的所有可能情况有:
(1)0,1,2,1,0.此时S(A5)=4;
(2)0,1,0,1,0.此时S(A5)=2;
(3)0,1,0,-1,0.此时S(A5)=0;
(4)0,-1,-2,-1,0.此时S(A5)=-4;
(5)0,-1,0,1,0.此时S(A5)=0;
(6)0,-1,0,-1,0.此时S(A5)=-2.
所以,S(A5)的所有可能取值为:-4,-2,0,2,4..…(5分)
(Ⅱ)由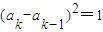 ,可设ak-ak-1=ck-1,则ck-1=1或ck-1=-1(2≤k≤n,k∈N*),a2-a1=c1,a3-a2=c2,
,可设ak-ak-1=ck-1,则ck-1=1或ck-1=-1(2≤k≤n,k∈N*),a2-a1=c1,a3-a2=c2,
…an-an-1=cn-1,
所以an=a1+c1+c2+…+cn-1. …(7分)
因为a1=an=0,所以c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由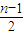 个1和
个1和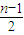 个-1构成的数列.
个-1构成的数列.
所以S(An)=c1+(c1+c2)+…+(c1+c2+…+cn-1)=(n-1)c1+(n-2)c2+…+2cn-2+cn-1.
则当c1,c2,…,cn-1的前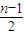 项取1,后
项取1,后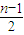 项取-1时S(An)最大,
项取-1时S(An)最大,
此时S(An)=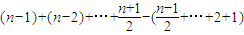 =
=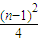 ..…(10分)
..…(10分)
证明如下:
假设c1,c2,…,cn-1的前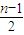 项中恰有t项
项中恰有t项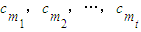 取-1,则c1,c2,…,cn-1的后
取-1,则c1,c2,…,cn-1的后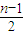 项中恰有t项
项中恰有t项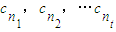 取1,其中
取1,其中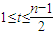 ,
,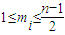 ,
,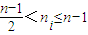 ,i=1,2,…,t.
,i=1,2,…,t.
所以S(An)=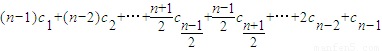 =
=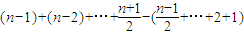 -2[(n-m1)+(n-m2)+…+(n-mt)]+2[(n-n1)+(n-n2)+…+(n-nt)]=
-2[(n-m1)+(n-m2)+…+(n-mt)]+2[(n-n1)+(n-n2)+…+(n-nt)]=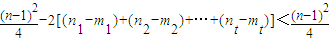 .
.
所以S(An)的最大值为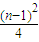 ..…(13分)
..…(13分)
点评:本题考查新定义,考查学生分析解决问题的能力,考查反证法的运用,难度较大.
(Ⅱ)由
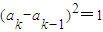 ,可设ak-ak-1=ck-1,可得an=a1+c1+c2+…+cn-1,根据a1=an=0,可得c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由
,可设ak-ak-1=ck-1,可得an=a1+c1+c2+…+cn-1,根据a1=an=0,可得c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由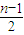 个1和
个1和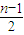 个-1构成的数列,由此可得当c1,c2,…,cn-1的前
个-1构成的数列,由此可得当c1,c2,…,cn-1的前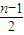 项取1,后
项取1,后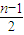 项取-1时S(An)最大.
项取-1时S(An)最大.解答:解:(Ⅰ)由题设,满足条件的数列A5的所有可能情况有:
(1)0,1,2,1,0.此时S(A5)=4;
(2)0,1,0,1,0.此时S(A5)=2;
(3)0,1,0,-1,0.此时S(A5)=0;
(4)0,-1,-2,-1,0.此时S(A5)=-4;
(5)0,-1,0,1,0.此时S(A5)=0;
(6)0,-1,0,-1,0.此时S(A5)=-2.
所以,S(A5)的所有可能取值为:-4,-2,0,2,4..…(5分)
(Ⅱ)由
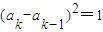 ,可设ak-ak-1=ck-1,则ck-1=1或ck-1=-1(2≤k≤n,k∈N*),a2-a1=c1,a3-a2=c2,
,可设ak-ak-1=ck-1,则ck-1=1或ck-1=-1(2≤k≤n,k∈N*),a2-a1=c1,a3-a2=c2,…an-an-1=cn-1,
所以an=a1+c1+c2+…+cn-1. …(7分)
因为a1=an=0,所以c1+c2+…+cn-1=0,且n为奇数,c1,c2,…,cn-1是由
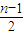 个1和
个1和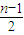 个-1构成的数列.
个-1构成的数列.所以S(An)=c1+(c1+c2)+…+(c1+c2+…+cn-1)=(n-1)c1+(n-2)c2+…+2cn-2+cn-1.
则当c1,c2,…,cn-1的前
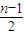 项取1,后
项取1,后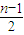 项取-1时S(An)最大,
项取-1时S(An)最大,此时S(An)=
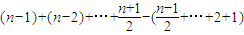 =
=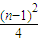 ..…(10分)
..…(10分)证明如下:
假设c1,c2,…,cn-1的前
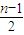 项中恰有t项
项中恰有t项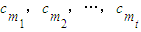 取-1,则c1,c2,…,cn-1的后
取-1,则c1,c2,…,cn-1的后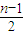 项中恰有t项
项中恰有t项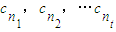 取1,其中
取1,其中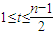 ,
,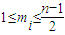 ,
,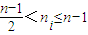 ,i=1,2,…,t.
,i=1,2,…,t.所以S(An)=
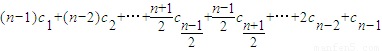 =
=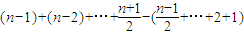 -2[(n-m1)+(n-m2)+…+(n-mt)]+2[(n-n1)+(n-n2)+…+(n-nt)]=
-2[(n-m1)+(n-m2)+…+(n-mt)]+2[(n-n1)+(n-n2)+…+(n-nt)]=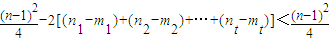 .
.所以S(An)的最大值为
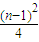 ..…(13分)
..…(13分)点评:本题考查新定义,考查学生分析解决问题的能力,考查反证法的运用,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目