题目内容
在平面区域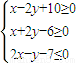 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M.
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M.(1)试求出圆M的方程;
(2)设过点P(0,3)作圆M的两条切线,切点分别记为A、B,又过P作圆N:x2+y2-4x+λy+4=0的两条切线,切点分别记为C、D,试确定λ的值,使AB⊥CD.
【答案】分析:(1)先画出该平面区域,明确区域所围成的平面图形的形状,再由“落在圆内的概率最大时的圆”则为该平面图形的内切圆.再由圆的相关条件求圆的方程.
(2)根据PM⊥AB,PN⊥CD,则要使AB⊥CD,只要PM⊥PN即可,即由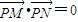 ,建立关于λ的方程来求解.
,建立关于λ的方程来求解.
解答:解:(1)画出该区域得三角形ABC,顶点坐标分别为A(-2,4),(4,1),(8,9),(2分)
且为直角三角形,三边长分别为3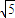 ,4
,4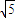 ,5
,5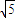 (4分)
(4分)
由于概率最大,故圆M是ABC内切圆,R=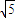 ,(5分)
,(5分)
设M(a,b),则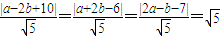 (7分)
(7分)
解得a=3,b=4(9分)
所以圆M的方程为(x-3)2+(y-4)2=5(10分)
(2)要使AB⊥CD,则PM⊥PN,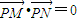 ,(13分)
,(13分)
N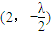 ,P(0,3)
,P(0,3)
求得λ=6(16分)
点评:本题主要考查平面区域的画法,三角形的内切圆的求法以及圆的切线的应用.还考查了数形结合的思想方法.
(2)根据PM⊥AB,PN⊥CD,则要使AB⊥CD,只要PM⊥PN即可,即由
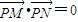 ,建立关于λ的方程来求解.
,建立关于λ的方程来求解.解答:解:(1)画出该区域得三角形ABC,顶点坐标分别为A(-2,4),(4,1),(8,9),(2分)
且为直角三角形,三边长分别为3
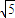 ,4
,4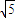 ,5
,5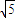 (4分)
(4分)由于概率最大,故圆M是ABC内切圆,R=
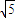 ,(5分)
,(5分)设M(a,b),则
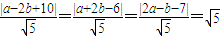 (7分)
(7分)解得a=3,b=4(9分)
所以圆M的方程为(x-3)2+(y-4)2=5(10分)
(2)要使AB⊥CD,则PM⊥PN,
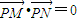 ,(13分)
,(13分)N
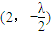 ,P(0,3)
,P(0,3)求得λ=6(16分)
点评:本题主要考查平面区域的画法,三角形的内切圆的求法以及圆的切线的应用.还考查了数形结合的思想方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
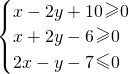 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M.
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M.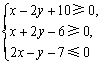 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M.
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M. 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M。
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为圆M。 内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为 .
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为 .