题目内容
7、已知命题:“若x⊥y,y∥z,则x⊥z”成立,那么字母x,y,z在空间所表示的几何图形不能( )
分析:本题考察的知识点是空间中直线与直线、直线与平面、平面与平面之间的位置判断,我们可根据空间中点、线、面之间的位置关系判定或性质定理对四个答案逐一进行分析,即可得到答案.
解答:解:若字母x,y,z在空间所表示的几何图形都是直线,
则由线线夹角的定义,我们易得两条平行线与第三条直线所成夹角相等,
故A不满足题意.
若字母x,y,z在空间所表示的几何图形都是平面
则由面面夹角的定义,我们易得两个平行平面与第三个平面所成夹角相等,
故B不满足题意.
若字母x,y,z在空间所表示的几何图形x,y是直线,z是平面
若x⊥y,y∥z,时,x也可能与z平行,
故C满足题意.
若字母x,y,z在空间所表示的几何图形x,z是平面,y是直线
则由面面垂直的判定定理易得结论正确
故D不满足题意.
则由线线夹角的定义,我们易得两条平行线与第三条直线所成夹角相等,
故A不满足题意.
若字母x,y,z在空间所表示的几何图形都是平面
则由面面夹角的定义,我们易得两个平行平面与第三个平面所成夹角相等,
故B不满足题意.
若字母x,y,z在空间所表示的几何图形x,y是直线,z是平面
若x⊥y,y∥z,时,x也可能与z平行,
故C满足题意.
若字母x,y,z在空间所表示的几何图形x,z是平面,y是直线
则由面面垂直的判定定理易得结论正确
故D不满足题意.
点评:线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知命题p:若x=y,则
=
,那么下列叙述正确的是( )
| x |
| y |
| A、命题p正确,其逆命题也正确 |
| B、命题p正确,其逆命题不正确 |
| C、命题p不正确,其逆命题正确 |
| D、命题p不正确,其逆命题也不正确 |
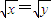 ,那么下列叙述正确的是( )
,那么下列叙述正确的是( )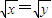 ,那么下列叙述正确的是( )
,那么下列叙述正确的是( )