题目内容
设（1+2x）n展开式的各项系数的和为an，各二项式系数的和为bn则lim
= ．
【答案】分析：利用给x赋值1得各项系数和，据二项式系数的性质得各二项式系数的和，代入求出极限值．
解答：解：对于（1+2x）n，令x=1得展开式的各项系数的和为3n
∴an=3n
又展开式中的二项式系数和为2n
∴bn=2n
∴
=
=
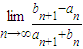故答案为
点评：本题考查赋值法求各项系数和；二项式系数和为2n；极限的求法．
解答：解：对于（1+2x）n，令x=1得展开式的各项系数的和为3n
∴an=3n
又展开式中的二项式系数和为2n
∴bn=2n
∴
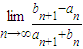==故答案为
点评：本题考查赋值法求各项系数和；二项式系数和为2n；极限的求法．
练习册系列答案
相关题目