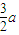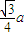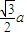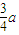题目内容
已知边长为a的菱形ABCD,∠A=
,将菱形ABCD沿对角线折成二面角θ,已知θ∈[
,
],则两对角线距离的最大值是( )
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:本题考查的知识点是空间点、线、面之间的距离计算,由处理空间问题的一般思路,我们要将空间问题转化为平面问题,由于本题中是将菱形ABCD沿对角线折成二面角,根据菱形对角线互相垂直的性质,我们易将二面角问题转化为平面角,进而求解.
解答:解:设菱形ABCD的对角线AC,BD相交于O点,
则由已知菱形ABCD边长的为a,∠A=
,
我们可得OA=OC=
a
又∵菱形的对角线互相垂直,
故∠AOC即为菱形ABCD沿对角线折成二面角
∴∠AOC=θ
则两对角线距离d=cos
•
a
又∵θ∈[
,
]
∴当θ=
时
d有最大值
a
故选D
则由已知菱形ABCD边长的为a,∠A=
| π |
| 3 |
我们可得OA=OC=
| ||
| 2 |
又∵菱形的对角线互相垂直,
故∠AOC即为菱形ABCD沿对角线折成二面角
∴∠AOC=θ
则两对角线距离d=cos
| θ |
| 2 |
| ||
| 2 |
又∵θ∈[
| π |
| 3 |
| 2π |
| 3 |
∴当θ=
| 2π |
| 3 |
d有最大值
| 3 |
| 4 |
故选D
点评:遇到二面角的问题,一般先作出二面角的平面角.我们可以利用二面角的平面角的定义作出∠AOC为二面角A-BD-C的平面角,通过解∠AOC所在的三角形求得两条异面直线之间的距离.

练习册系列答案
相关题目
 ,将菱形ABCD沿对角线折成二面角θ,已知θ∈[
,将菱形ABCD沿对角线折成二面角θ,已知θ∈[ ],则两对角线距离的最大值是
],则两对角线距离的最大值是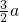

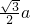

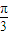 ,将菱形ABCD沿对角线折成二面角θ,已知θ∈[
,将菱形ABCD沿对角线折成二面角θ,已知θ∈[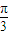 ,
,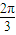 ],则两对角线距离的最大值是( )
],则两对角线距离的最大值是( )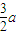
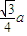
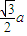
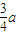
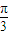 ,将菱形ABCD沿对角线折成二面角θ,已知θ∈[
,将菱形ABCD沿对角线折成二面角θ,已知θ∈[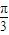 ,
,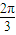 ],则两对角线距离的最大值是( )
],则两对角线距离的最大值是( )