题目内容
(1)(矩阵与变换)已知二阶矩阵M=
.
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)设向量
=
,求M100
.
(2)(坐标系与参数方程)
已知曲线C1的参数方程为
(θ是参数),曲线C2的极坐标方程为θ=
(ρ∈R).
(Ⅰ)求曲线C1的普通方程和曲线C2的平面直角坐标方程;
(Ⅱ)设曲线C1和曲线C2相交于A,B两点,求弦长|AB|.
|
(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)设向量
| α |
|
| α |
(2)(坐标系与参数方程)
已知曲线C1的参数方程为
|
| π |
| 4 |
(Ⅰ)求曲线C1的普通方程和曲线C2的平面直角坐标方程;
(Ⅱ)设曲线C1和曲线C2相交于A,B两点,求弦长|AB|.
分析:(1)(Ⅰ)二阶矩阵M=
.由(M|I)=
→
→
,能求出M-1=
.
(Ⅱ)由特征值λ1=1,λ2=2,特征向量
=
,
=
,知
=
+2
,由此能求出M100
.
(2)(Ⅰ)由线C1的参数方程为
(θ是参数),曲线C2的极坐标方程为θ=
(ρ∈R),能求出曲线C1的普通方程和曲线C2的平面直角坐标方程.
(Ⅱ)由圆心(1,-1)到直线y=x的距离d=
=
,圆半径r=2,能求出弦长|AB|.
|
|
|
|
|
|
|
|
(Ⅱ)由特征值λ1=1,λ2=2,特征向量
| ξ1 |
|
| ξ2 |
|
| α |
| ξ1 |
| ξ2 |
| α |
(2)(Ⅰ)由线C1的参数方程为
|
| π |
| 4 |
(Ⅱ)由圆心(1,-1)到直线y=x的距离d=
| |1+1| | ||
|
| 2 |
解答:解:(1)(Ⅰ)∵二阶矩阵M=
.
∴(M|I)=(
|
)→(
)
→
→
,
∴M-1=
;
(Ⅱ)∵特征值λ1=1,λ2=2,
特征向量
=
,
=
,
所以
=
+2
,
所以M100
=M100(
+2
)=λ1100
+2λ2100
=
.
(2)(Ⅰ)∵线C1的参数方程为
(θ是参数),
曲线C2的极坐标方程为θ=
(ρ∈R).
曲线的普通方程C1:(x-1)2+(y+1)2=4,
曲线C2的普通方程:y=x;
(Ⅱ)∵圆心(1,-1)到直线y=x的距离d=
=
,
圆半径r=2,
∴弦长|AB|=2
=2
.
|
∴(M|I)=(
|
|
|
|
→
|
|
|
|
∴M-1=
|
(Ⅱ)∵特征值λ1=1,λ2=2,
特征向量
| ξ1 |
|
| ξ2 |
|
所以
| α |
| ξ1 |
| ξ2 |
所以M100
| α |
| ξ1 |
| ξ2 |
| ξ1 |
| ξ2 |
|
(2)(Ⅰ)∵线C1的参数方程为
|
曲线C2的极坐标方程为θ=
| π |
| 4 |
曲线的普通方程C1:(x-1)2+(y+1)2=4,
曲线C2的普通方程:y=x;
(Ⅱ)∵圆心(1,-1)到直线y=x的距离d=
| |1+1| | ||
|
| 2 |
圆半径r=2,
∴弦长|AB|=2
| 4-2 |
| 2 |
点评:第(1)题考查逆矩阵的求法和特征根、特征值的求法;第(2)题考查曲线的参数方程的应用和弦长的计算.是基础题,解题时要认真审题,仔细解答.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
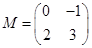
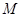 的
的 逆矩阵;
逆矩阵; ,求
,求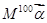
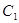 的参数方程为
的参数方程为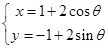 (
(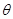 是参数),曲线
是参数),曲线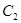 的极坐标方程为
的极坐标方程为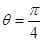 (
(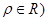 .
. 求曲线
求曲线 (Ⅱ)设曲线
(Ⅱ)设曲线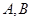 两点,求弦长
两点,求弦长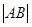
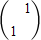 ,N=
,N=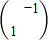 ,求△ABC在矩阵MN作用下变换所得的图形的面积;
,求△ABC在矩阵MN作用下变换所得的图形的面积;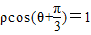 与圆
与圆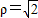 的公共点个数;
的公共点个数;