题目内容
已知函数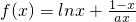 ,其中a为大于零的常数.
,其中a为大于零的常数.
(I)若函数f(x)在区间[1,+∞)内单调递增,求a的取值范围;
(II)设函数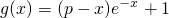 ,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求实数p的取值范围.(e为自然对数的底)
,若存在x0∈[1,e],使不等式g(x0)≥lnx0成立,求实数p的取值范围.(e为自然对数的底)
解:(I)f′(x)=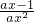 (x>0),令f′(x)=0,得x=
(x>0),令f′(x)=0,得x= ,
,
所以在(0, ]上f′(x)≤0,在[
]上f′(x)≤0,在[ ,+∞)上f′(x)≥0,
,+∞)上f′(x)≥0,
所以f(x)在(0, ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增,
,+∞)上单调递增,
因为函数f(x)在区间[1,+∞)内单调递增,
所以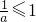 ,又a>0,所以a≥1,
,又a>0,所以a≥1,
所以所求实数a的取值范围为[1,+∞);
(II)存在x0∈[1,e]使g(x0)≥lnx0,即存在x0∈[1,e]使p≥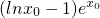 +x0成立,
+x0成立,
令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),
h′(x)=(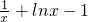 )ex+1,
)ex+1,
由(I)知当a≥1且x≥1时,f(x)=lnx+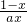 ≥f(1)=0成立,
≥f(1)=0成立,
所以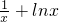 -1≥0在[1,e]上成立,
-1≥0在[1,e]上成立,
所以h′(x)= +1≥1+1>0,
+1≥1+1>0,
所以h(x)=(lnx-1)ex+x在[1,e]上单调递增,
所以hmin(x)=h(1)=1-e,
所以p≥1-e.
分析:(I)求导数f′(x),利用导数求出f(x)的增区间,由f(x)在区间[1,+∞)内单调递增,得[1,+∞)为f(x)增区间的子集,由此得不等式,解出即可;
(II)存在x0∈[1,e]使g(x0)≥lnx0,即存在x0∈[1,e]使p≥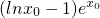 +x0成立,令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),由(I)可判断h′(x)>0,从而h(x)在[1,e]上递增,进而得h(x)的最小值,从而问题可解;
+x0成立,令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),由(I)可判断h′(x)>0,从而h(x)在[1,e]上递增,进而得h(x)的最小值,从而问题可解;
点评:本题考查利用导数研究函数的单调性、最值,考查转化思想,要准确理解“恒成立问题”与“能成立问题”的区别联系并能恰当转化.
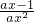 (x>0),令f′(x)=0,得x=
(x>0),令f′(x)=0,得x= ,
,所以在(0,
 ]上f′(x)≤0,在[
]上f′(x)≤0,在[ ,+∞)上f′(x)≥0,
,+∞)上f′(x)≥0,所以f(x)在(0,
 ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增,
,+∞)上单调递增,因为函数f(x)在区间[1,+∞)内单调递增,
所以
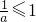 ,又a>0,所以a≥1,
,又a>0,所以a≥1,所以所求实数a的取值范围为[1,+∞);
(II)存在x0∈[1,e]使g(x0)≥lnx0,即存在x0∈[1,e]使p≥
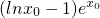 +x0成立,
+x0成立,令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),
h′(x)=(
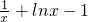 )ex+1,
)ex+1,由(I)知当a≥1且x≥1时,f(x)=lnx+
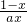 ≥f(1)=0成立,
≥f(1)=0成立,所以
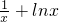 -1≥0在[1,e]上成立,
-1≥0在[1,e]上成立,所以h′(x)=
 +1≥1+1>0,
+1≥1+1>0,所以h(x)=(lnx-1)ex+x在[1,e]上单调递增,
所以hmin(x)=h(1)=1-e,
所以p≥1-e.
分析:(I)求导数f′(x),利用导数求出f(x)的增区间,由f(x)在区间[1,+∞)内单调递增,得[1,+∞)为f(x)增区间的子集,由此得不等式,解出即可;
(II)存在x0∈[1,e]使g(x0)≥lnx0,即存在x0∈[1,e]使p≥
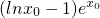 +x0成立,令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),由(I)可判断h′(x)>0,从而h(x)在[1,e]上递增,进而得h(x)的最小值,从而问题可解;
+x0成立,令h(x)=(lnx-1)ex+x,从而p≥hmin(x)(x∈[1,e]),由(I)可判断h′(x)>0,从而h(x)在[1,e]上递增,进而得h(x)的最小值,从而问题可解;点评:本题考查利用导数研究函数的单调性、最值,考查转化思想,要准确理解“恒成立问题”与“能成立问题”的区别联系并能恰当转化.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
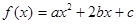 ,其中a≥b>c,a+b+c=0.
,其中a≥b>c,a+b+c=0.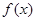 有两个零点;
有两个零点;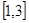 上的最小值为1,最大值为13,求a、b、c的值.
上的最小值为1,最大值为13,求a、b、c的值.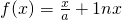 ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数.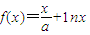 ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数.