题目内容
复数z1=2i，z2=1-i，（其中i为虚数单位），
（1）求
，
（2）复平面上，z1，z2分别对应点Z1，Z2，O是原点，以OZ1，OZ2为两邻边的平行四边形，求这个平行四边形的两条对角线的长度．
（1）求
| z1 |
| z2 |
（2）复平面上，z1，z2分别对应点Z1，Z2，O是原点，以OZ1，OZ2为两邻边的平行四边形，求这个平行四边形的两条对角线的长度．
（1）
=
=
=
=-1+i．
（2）∵z1+z2=2i+1-i=1+i；z1-z2=2i-（1-i）=-1+3i．
∴|z1+z2|=
=
，|z1-z2|=
=
．
∴这个平行四边形的两条对角线的长度分别为
，
．
| z1 |
| z2 |
| 2i |
| 1-i |
| 2i(1+i) |
| (1-i)(1+i) |
| 2(-1+i) |
| 2 |
（2）∵z1+z2=2i+1-i=1+i；z1-z2=2i-（1-i）=-1+3i．
∴|z1+z2|=
| 12+12 |
| 2 |
| (-1)2+32 |
| 10 |
∴这个平行四边形的两条对角线的长度分别为
| 2 |
| 10 |
练习册系列答案
相关题目
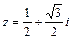,则
（ ）
，
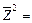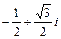
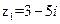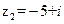，则复数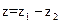
在复平面内所表示的点位于第 象限. 
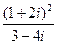的值是( )