题目内容
已知P(x,y)是圆x2+(y-3)2=1上的动点,定点A(2,0),B(-2,0),则
•
的最大值为( )
| PA |
| PB |
| A、12 | B、0 | C、-12 | D、4 |
分析:由平面向量的数量积公式,可得
•
的解析式;再由P(x,y)是圆x2+(y-3)2=1上的动点,可得x,y的取值范围;从而求得
•
的最大值(或最小值).
| PA |
| PB |
| PA |
| PB |
解答:解:∵P(x,y)是圆x2+(y-3)2=1上的动点,且A(2,0),B(-2,0),
∴
•
=(2-x,0-y)•(-2-x,0-y)=(2-x)•(-2-x)+(-y)2=x2+y2-4,
由x2+(y-3)2=1,得x2+y2=6y-8,且2≤y≤4,∴x2+y2-4=6y-12≤24-12=12,
∴
•
的最大值为:12
故答案选:A.
∴
| PA |
| PB |
由x2+(y-3)2=1,得x2+y2=6y-8,且2≤y≤4,∴x2+y2-4=6y-12≤24-12=12,
∴
| PA |
| PB |
故答案选:A.
点评:本题考查了平面向量的数量积和圆的解析方程等有关知识,是基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 的最大值为( )
的最大值为( )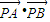 的最大值为( )
的最大值为( ) 的最大值为( )
的最大值为( )